
【题目】如图,地物线点![]() :
:![]() (
(![]() 、
、![]() 、
、![]() 均不为0)的顶点为
均不为0)的顶点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,我们称以
,我们称以![]() 为顶点,对称轴是
为顶点,对称轴是![]() 轴且过点
轴且过点![]() 的抛物线为抛物线
的抛物线为抛物线![]() 的衍生抛物线,直线
的衍生抛物线,直线![]() 为抛物线
为抛物线![]() 的衍生直线.
的衍生直线.
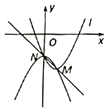
(1)求抛物线![]() 的衍生抛物线和衍生直线的解析式;
的衍生抛物线和衍生直线的解析式;
(2)若一条抛物线的衍生抛物线和衍生直线分别是![]() 和
和![]() ,求这条抛物线的解析式.
,求这条抛物线的解析式.
【答案】(1)![]() ;
;![]() (2)
(2)![]()
【解析】
(1)衍生抛物线顶点为原抛物线与y轴的交点,则可根据顶点设顶点式方程,由衍生抛物线过原抛物线的顶点代入顶点坐标可求出衍生抛物线解析式.根据衍生直线经过M、N可求衍生直线的解析式.
(2)已知衍生抛物线和衍生直线求原抛物线思路正好与(1)相反,根据衍生抛物线与衍生直线的两交点分别为衍生抛物线与原抛物线的交点,则可推得原抛物线顶点式,再代入经过点,即得解析式.
解:(1)∵抛物线![]() 点过
点过![]() ,
,
∴设其衍生抛物线为![]() .
.
∵![]() ,
,
∴衍生抛物线![]() 过抛物线
过抛物线![]() 的顶点
的顶点![]() .
.
∴![]() ,即
,即![]() .
.
∴衍生抛物线为![]() .
.
设衍生直线为![]() ,则直线
,则直线![]() 点过
点过![]() 与
与![]() ,
,
∴![]() 解得
解得![]()
∴衍生直线为![]() .
.
(2)∵衍生抛物线和衍生直线两交点分别为原抛物线与衍生抛物线的顶点,
∴将![]() 和
和![]() 联立,得
联立,得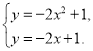
解得![]() 或
或![]()
∵衍生抛物线![]() 的顶点为
的顶点为![]() ,
,
∴原抛物线的顶点为![]() .
.
设原抛物线为![]() ,则抛物线
,则抛物线![]() 过点
过点![]() ,
,
∴![]() ,即
,即![]() ,
,
∴原抛物线为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
(1)求证:AE是⊙O的切线;
(2) 连接OC,当BC=3时,求劣弧AC的长和扇形B0C的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
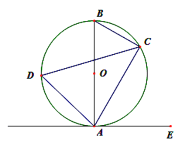
【题目】如图1,在平面直角坐标系中,抛物线![]() 经过点
经过点![]() 和点
和点![]() .
.
(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)点![]() 是抛物线上
是抛物线上![]() 、
、![]() 之间的一点,过点
之间的一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,当矩形
,当矩形![]() 的周长最大时,求点
的周长最大时,求点![]() 的横坐标;
的横坐标;
(3)如图2,连接![]() 、
、![]() ,点
,点![]() 在线段
在线段![]() 上(不与
上(不与![]() 、
、![]() 重合),作
重合),作![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() ,是否存在这样点
,是否存在这样点![]() ,使得
,使得![]() 为等腰三角形?若存在,求出
为等腰三角形?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为5的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
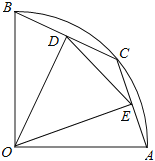
(1)当BC=6时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学课上,张老师出示了一个题目:“如图,ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,![]() 请根据上述条件,写出一个正确结论
请根据上述条件,写出一个正确结论![]() ”其中四位同学写出的结论如下:
”其中四位同学写出的结论如下:
小青:![]() ;小何:四边形DFBE是正方形;
;小何:四边形DFBE是正方形;
小夏:![]() ;小雨:
;小雨:![]() .
.
这四位同学写出的结论中不正确的是![]()
![]()

A. 小青 B. 小何 C. 小夏 D. 小雨
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com