

分析 (1)依据等腰三角形的性质得到AB=AC,AD=AE,依据同角的余角相等得到∠DAB=∠CAE,然后依据SAS可证明△ADB≌△AEC,最后,依据全等三角形的性质可得到BD=CE;
(2)分为点E在AB上和点E在AB的延长线上两种情况画出图形,然后再证明△PEB∽△AEC,最后依据相似三角形的性质进行证明即可.
解答 解:(1)∵△ABC和△ADE是等腰直角三角形,∠BAC=∠DAE=90°,
∴AB=AC,AD=AE,∠DAB=∠CAE.
∴△ADB≌△AEC.
∴BD=CE.
(2)解:①当点E在AB上时,BE=AB-AE=1.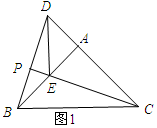
∵∠EAC=90°,
∴CE=$\sqrt{A{E}^{2}+A{C}^{2}}$=$\sqrt{5}$.
同(1)可证△ADB≌△AEC.
∴∠DBA=∠ECA.
∵∠PEB=∠AEC,
∴△PEB∽△AEC.
∴$\frac{PB}{AC}$=$\frac{BE}{CE}$.
∴$\frac{PB}{2}$=$\frac{1}{\sqrt{5}}$.
∴PB=$\frac{2\sqrt{5}}{5}$.
②当点E在BA延长线上时,BE=3.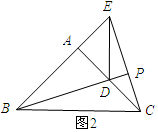
∵∠EAC=90°,
∴CE=$\sqrt{A{E}^{2}+A{C}^{2}}$=$\sqrt{5}$.
同(1)可证△ADB≌△AEC.
∴∠DBA=∠ECA.
∵∠BEP=∠CEA,
∴△PEB∽△AEC.
∴$\frac{PB}{AC}$=$\frac{BE}{CE}$.
∴$\frac{PB}{2}$=$\frac{3}{\sqrt{5}}$.
∴PB=$\frac{6\sqrt{5}}{5}$.
综上所述,PB的长为$\frac{2\sqrt{5}}{5}$或$\frac{6\sqrt{5}}{5}$.
点评 本题主要考查的是旋转的性质、等腰三角形的性质、全等三角形的性质和判定、相似三角形的性质和判定,证明得△PEB∽△AEC是解题的关键.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
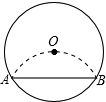 如图将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )
如图将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )| A. | 2cm | B. | $\sqrt{3}$cm | C. | 2$\sqrt{5}$cm | D. | 2$\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
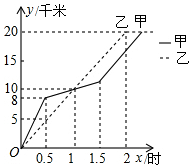 在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,有下列说法:
在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,有下列说法:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com