
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E是AC的中点,OE交CD于点F.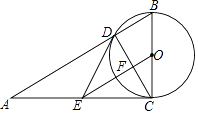
(1)若∠BCD=36°,BC=10,求BD的长;
(2)判断直线DE与⊙O的位置关系,并说明理由;
(3)求证:2CE2=ABEF.
【答案】
(1)解:∵BC是直径,
∴∠BDC=90°,
在Rt△BCD中,∵BC=10,∠BCD=36°,
∴BD=BCsin36°=10sin36°≈5.9.
(2)解:连接OD.
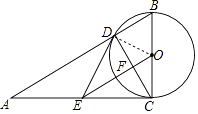
∵AE=EC,OB=OC,
∴OE∥AB,
∵CD⊥AB,
∴OE⊥CD,
∵OD=OC,
∴∠DOE=∠COE,
在△EOD和△EOC中,
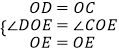 ,
,
∴△EOD≌△EOC,
∴∠EDO=∠ECO=90°,
∴OD⊥DE,
∴DE是⊙O的切线.
(3)解:∵OE⊥CD,
∴DF=CF,∵AE=EC,
∴AD=2EF,
∵∠CAD=∠CAB,∠ADC=∠ACB=90°,
∴△ACD∽△ABC,
∴AC2=ADAB,
∵AC=2CE,
∴4CE2=2EFAB,
∴2CE2=EFAB.
【解析】(1)在直角三角形中,由斜边求对边,用正弦;(2)要证DE是切线,连结OE,证∠EDO是直角,可证△EOD≌△EOC,得出∠EDO=∠ECO=90°;(3)要证2CE2=ABEF,可从![]() 入手,CE2=
入手,CE2=![]() ,所以2CE2=2
,所以2CE2=2![]()
【考点精析】解答此题的关键在于理解直线与圆的三种位置关系的相关知识,掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是菱形,DF⊥AB于点F,BE⊥CD于点E.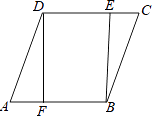
(1)求证:AF=CE;
(2)若DE=2,BE=4,求sin∠DAF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A![]() 点B
点B![]() 已知
已知![]() 满足
满足![]() .
.
(1)点A的坐标为_________,点B的坐标为__________;
(2)如图1,点E为线段OB上一点,连接AE,过A作AF⊥AE,且AF=AE,连接BF交![]() 轴于点D,若点D(-1,0),求点E的坐标;
轴于点D,若点D(-1,0),求点E的坐标;
(3)在(2)的条件下,如图2,过E作EH⊥OB交AB于H,点M是射线EH上一点(点M不在线段EH上),连接MO,作∠MON=45°,ON交线段BA的延长线于点N,连接MN,探究线段MN与OM的关系,并说明理由。
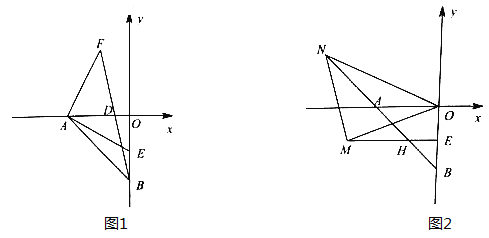
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积.方法1:______;方法2:_______.
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系._______;
(3)类似的,请你用图1中的三种纸片拼一个使长方形面积为:3a2+7ab+2b2,并对3a2+7ab+2b2因式分解为_______.
(4)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(x﹣2016)2+(x﹣2018)2=34,求(x﹣2017)2的值.
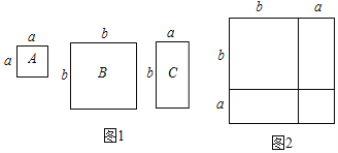
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.甲、乙两种商品原来的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC沿着点A到点D的方向平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)画出△ABC中AB边上的高CH;(提醒:别忘了标注字母);
(2)请画出平移后的△DEF;
(3)平移后,线段AB扫过的部分所组成的封闭图形的面积是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车制造厂开发了一款新式电动汽车,计划一年生产安装240辆。由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人:他们经过培训后上岗,也能独立进行电动汽车的安装。生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车。
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘新工人若干名(新工人人数少于10人)和抽调的熟练工合作,刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市电力部门对一般照明用电实行“阶梯电价”收费,具体收费标准如下:
第一档:月用电量不超过200度的部分的电价为每度![]() 元.
元.
第二档:月用电量超过200度但不超过400度部分的电价为每度![]() 元.
元.
第三档:月用电量超过400度的部分的电价为每度![]() 元.
元.
![]() 已知小明家去年5月份的用电量为215度,则小明家5月份应交电费______元
已知小明家去年5月份的用电量为215度,则小明家5月份应交电费______元![]()
![]() 若去年6月份小明家用电的平均电价为
若去年6月份小明家用电的平均电价为![]() 元,求小明家去年6月份的用电量.
元,求小明家去年6月份的用电量.
![]() 已知小明家去年7、8月份的用电量共700度
已知小明家去年7、8月份的用电量共700度![]() 月份的用电量少于8月份的用电量
月份的用电量少于8月份的用电量![]() ,两个月的总电价是384元,求小明家7、8月的用电量分别是多少?
,两个月的总电价是384元,求小明家7、8月的用电量分别是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com