练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．在△ABC中，DE∥BC交AB于D，交AC于E，且AD：DB=2：3，△ABC的周长为27cm，求△ADE的周长．

    分析 由于DE∥BC，易证得△ADE∽△ABC；已知了AD、DB的比例关系，即可得到两个三角形的相似比，根据相似三角形的周长比等于相似比即可得解．

    解答 解：∵DE∥BC，
    ∴△ADE∽△ABC；
    ∴C△ADE：C△ABC=AD：AB，
    ∵AD：DB=2：3，
    ∴AD：AB=2：5；
    即△ADE的周长与△ABC的周长的比为$\frac{2}{5}$，
    ∵△ABC的周长为27cm，
    ∴△ADE的周长=$\frac{54}{5}$．

    点评 本题考查了相似三角形的判定与性质，根据相似三角形周长的比等于相似比解决问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    15．下列等式成立的是（　　）
    A．$\frac{a}{b}$=$\frac{{a}^{2}}{{b}^{2}}$B．$\frac{a}{b}$=$\frac{a+c}{b+c}$C．$\frac{a}{b}$=$\frac{a-c}{b-c}$D．$\frac{a}{b}$=$\frac{ma}{mb}$（m≠0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

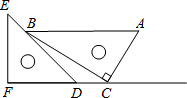    16．一副直角三角板如图放置，点C在FD的延长线上，AB∥CF，∠F=∠ACB=90°，∠E=45°，∠A=60°，AC=2，则CD的长为3-$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．如图，正方形EFMN内接于△ABC，BC=18，BC边上的高AD=12，则正方形EFMN的边长为$\frac{24}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．矩形ABCD的边长AD=3，AB=2，E为AB的中点，F在线段BC上，F在线段BC上，且BF：FC=1：2，AF分别与DE，DB交于点M，N，则MN=（　　）
    A．$\frac{3\sqrt{5}}{7}$B．$\frac{5\sqrt{5}}{14}$C．$\frac{9\sqrt{5}}{28}$D．$\frac{11\sqrt{5}}{28}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，是某油田的四口油井的位置图，图中1cm表示实际距离1.5km．请你仔细观察，并量一量图中的距离，用语言叙述这四口油井之间的位置关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

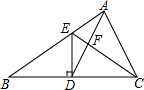    17．如图，在△ABC中，D是BC边上的中点，AD=AC，DE⊥BC，交AB于点E，CE与AD相交于点F，BC=10，S△CDF=6．
    ①求证：△ABC∽△FCD．
    ②求△ABC的面积S△ABC．
    ③求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

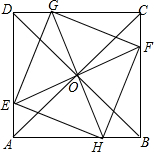    14．已知；如图，在正方形ABCD中，AC与BD相交于点O，EF，GH都过点O，分别交AD，BC于E，F，交CD，AB于G，H，EF⊥GH，求证：四边形EHFG是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

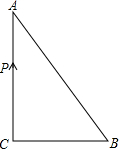    11．如图，在Rt△ABC中，∠C=90°，BC=6cm，CA=8cm，动点P从点C出发，以2cm/s的速度沿CA、AB移动到B，则点P出发（　　）时，可使S△BCP=$\frac{1}{4}$S△ABC．
    A．1sB．$\frac{31}{4}$sC．1s或$\frac{31}{4}$sD．2s

    查看答案和解析>>

    同步练习册答案