
【题目】如图,已知线段AB=12,点M、N是线段AB上的两点,且AM=BN=2,点P是线段MN上的动点,分别以线段AP、BP为边在AB的同侧作正方形APDC、正方形PBFE,点G、H分别是CD、EF的中点,点O是GH的中点,当P点从M点到N点运动过程中,OM+OB的最小值是( )

A.10B.12C.2 ![]() D.12
D.12![]()
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠B=60°,点E、F分别从点B、D出发以同样的速度沿边BC、DC向点C运动.给出以下四个结论:

①AE=AF;
②∠CEF=∠CFE;
③当点E,F分别为边BC,DC的中点时,△AEF是等边三角形;
④当点E,F分别为边BC,DC的中点时,△AEF的面积最大.
上述结论中正确的序号有 .(把你认为正确的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系式示意图.根据图中提供的信息回答下列问题:
(1)小红家到舅舅家的路程是______米,小红在商店停留了______分钟;
(2)在整个去舅舅家的途中哪个时间段小红骑车速度最快,最快的速度是多少米/分
(3)本次去舅舅家的行程中,小红一共行驶了多少米?一共用了多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连结EC.
(1)求证:AD=EC;
(2)求证:四边形ADCE是菱形;
(3)若AB=AO,求![]() 的值.
的值.
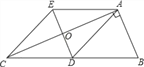
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某淘宝商家计划平均每天销售某品牌儿童滑板车 ![]() 辆,但由于种种原因,实际每天的销售量与计划量相比有差距.下表是某周的销售情况(超额记为正、不足记为负):
辆,但由于种种原因,实际每天的销售量与计划量相比有差距.下表是某周的销售情况(超额记为正、不足记为负):

(1)根据记录的数据可知该店前三天共销售该品牌儿童滑板车 辆;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 辆;
(3)通过计算说明:本周实际销售总量达到了计划数量没有?
(4)该店实行每日计件工资制,每销售一辆车可得 ![]() 元,若超额完成任务,则超过部分每辆另奖
元,若超额完成任务,则超过部分每辆另奖![]() 元;少销售一辆扣
元;少销售一辆扣 ![]() 元,那么该店铺的销售人员这一周的工资总额是多少元?
元,那么该店铺的销售人员这一周的工资总额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读对人成长的影响是巨大的,一本好书往往能改变人的一生,每年的4月23日被联合国教科文组织确定为“世界读书日”.蓝天中学为了解八年级学生本学期的课外阅读情况,随机抽查部分学生对其课外阅读量进行统计分析,绘制成两幅不完整的统计图.根据图示信息,解答下列问题:
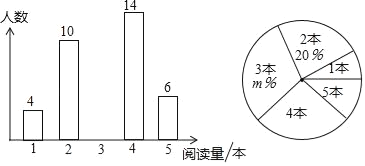
(1)求被抽查学生人数,课外阅读量的众数,扇形统计图中m的值;并将条形统计图补充完整;
(2)若规定:本学期阅读3本以上(含3本)课外书籍者为完成目标,据此估计该校600名学生中能完成此目标的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售一种新型节能产品,现准备从国内和国外两种销售方案中选择一种进行销售.若只在国内销售,销售价格y(元/件)与月销量x(件)的函数关系式为y =![]() x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元)(利润=销售额-成本-广告费).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元)(利润=销售额-成本-广告费).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳![]() x2元的附加费,设月利润为w外(元)(利润=销售额-成本-附加费).
x2元的附加费,设月利润为w外(元)(利润=销售额-成本-附加费).
(1)当x=1000时,y= 元/件,w内= 元;
(2)分别求出w内,w外与x间的函数关系式(不必写x的取值范围);
(3)当x为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值;
(4)如果某月要将5000件产品全部销售完,请你通过分析帮公司决策,选择在国内还是在国外销售才能使所获月利润较大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点E、F分别是四边形ABCD边AB、AD上的点,且DE与CF相交于点G.
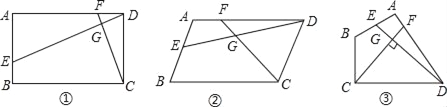
(1)如图①,若AB∥CD,AB=CD,∠A=90°,且ADDF=AEDC,求证:DE⊥CF:
(2)如图②,若AB∥CD,AB=CD,且∠A=∠EGC时,求证:DECD=CFDA:
(3)如图③,若BA=BC=3,DA=DC=4,设DE⊥CF,当∠BAD=90°时,试判断![]() 是否为定值,并证明.
是否为定值,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
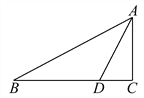
【题目】如图,已知在Rt△ABC中,∠C=90°,D是BC边上一点,AC=6,CD=3,∠ADC=α.
(1)试写出α的正弦、余弦、正切这三个函数值;
(2)若∠B与∠ADC互余,求BD及AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com