
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
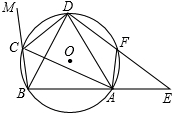 如图,△ABC内接于圆,∠BCA外角的平分线CD交该圆于点D,F为弧AD上一点,连接并延长DF与BA的延长线交于点E.连结BD,AF.
如图,△ABC内接于圆,∠BCA外角的平分线CD交该圆于点D,F为弧AD上一点,连接并延长DF与BA的延长线交于点E.连结BD,AF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 月用水量 | 不超过12方的部分 | 超过12方不超过18方的部分 | 超过18方的部分 |
| 收费标准(元/方) | 2 | 2.5 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{2x-y=-3}\\{4x+y=6}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x-y=-6}\\{2x+y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=0}\\{x-y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+y=-2}\\{x+2y=2}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知四边形ABCD中,∠A+∠DCB=180°,两组对边延长后,分别交于P、Q两点,∠APD、∠AQB的平分线交于M,求证:PM⊥QM.
如图,已知四边形ABCD中,∠A+∠DCB=180°,两组对边延长后,分别交于P、Q两点,∠APD、∠AQB的平分线交于M,求证:PM⊥QM.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com