
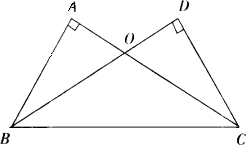
如图,∠A=∠D=90°,AC=BD,能说明△OBC是等腰三角形吗?
科目:初中数学 来源:新教材新学案 数学 七年级下册 题型:022
如图,∠BAM=75°,∠BGE=75°,∠CHG=105°,可推出AM∥EF,AB∥CD.试完成下列填空:

解:因为∠BAM=75°,∠BGE=75°(已知)
所以∠BAM=∠BGE( )
所以AM∥EF( )
又因为∠AGH=∠BGE( )
所以∠AGH=75°( )
所以∠AGH+∠CHG=75°+105°=180°
所以________∥________( )
查看答案和解析>>
科目:初中数学 来源:活学巧练 八年级数学 下 题型:013
如图,∠1=![]() ,∠2=
,∠2=![]() ,∠3=
,∠3=![]() ,则∠4=
,则∠4=![]() .下面是A,B,C,D四个同学的推理过程.你认为推理正确的是
.下面是A,B,C,D四个同学的推理过程.你认为推理正确的是

[ ]
A.因为∠1=![]() =∠2,所以a∥b,所以∠4=∠3=
=∠2,所以a∥b,所以∠4=∠3=![]()
B.因为∠4=![]() =∠3,所以a∥b,故∠1=∠2=
=∠3,所以a∥b,故∠1=∠2=![]()
C.因为∠2=∠5,又∠1=![]() ,∠2=
,∠2=![]() ,故∠1=∠5=
,故∠1=∠5=![]() .所以a∥b,所以∠4=∠3=
.所以a∥b,所以∠4=∠3=![]()
D.因为∠1=![]() ,∠2=
,∠2=![]() ,∠3=
,∠3=![]() ,所以∠1-∠3=∠2-∠4=
,所以∠1-∠3=∠2-∠4=![]() -
-![]() =
=![]() ,故∠4=
,故∠4=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
在课外小组活动时,小伟拿来一道题(原问题)和小熊、小强交流.
原问题:如图1,已知△ABC,∠ACB=90° , ∠ABC=45°,分别以AB、BC为边向外作△ABD与△BCE, 且DA=DB, EB=EC,∠ADB=∠BEC=90°,连接DE交AB于点F. 探究线段DF与EF的数量关系.小伟同学的思路是:过点D作DG⊥AB于G,构造全等三角形,通过推理使问题得解.小熊同学说:我做过一道类似的题目,不同的是∠ABC=30°,∠ADB=∠BEC=60°.小强同学经过合情推理,提出一个猜想,我们可以把问题推广到一般情况.请你参考小慧同学的思路,探究并解决这三位同学提出的问题:
1.写出原问题中DF与EF的数量关系
2.如图2,若∠ABC=30°,∠ADB=∠BEC=60°,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明;
3.如图3,若∠ADB=∠BEC=2∠ABC,原问题中的其他条件不变,你在(1)中

得到的结论是否发生变化?请写出你的猜想并加以证明
查看答案和解析>>
科目:初中数学 来源:2012年北师大版初中数学八年级下6.1你能肯定吗练习卷(解析版) 题型:选择题
如图,∠1=60º,∠2=60º,∠3=57º,则∠4=57º,下面是A,B,C,D四个同学的推理过程,你认为推理正确的是( )

A.因为∠1=60º=∠2,所以a∥b,所以∠4=∠3=57º
B.因为∠4=57º=∠3,所以a∥b,故∠1=∠2=60º
C.因为∠2=∠5,又∠1=60º,∠2=60º,故∠1=∠5=60º,所以a∥b,所以∠4=∠3=57º
D.因为∠1=60º,∠2=60º,∠3=57º,所以∠1=∠3=∠2-∠4=60º-57º=3º,
故∠4=57º
查看答案和解析>>
科目:初中数学 来源:2011-2012学年四川乐山市区中考模拟数学试卷(解析版) 题型:解答题
在课外小组活动时,小伟拿来一道题(原问题)和小熊、小强交流.
原问题:如图1,已知△ABC, ∠ACB=90° , ∠ABC=45°,分别以AB、BC为边向外作△ABD与△BCE, 且DA=DB, EB=EC,∠ADB=∠BEC=90°,连接DE交AB于点F. 探究线段DF与EF的数量关系.小伟同学的思路是:过点D作DG⊥AB于G,构造全等三角形,通过推理使问题得解.小熊同学说:我做过一道类似的题目,不同的是∠ABC=30°,∠ADB=∠BEC=60°.小强同学经过合情推理,提出一个猜想,我们可以把问题推广到一般情况.请你参考小慧同学的思路,探究并解决这三位同学提出的问题:
1.写出原问题中DF与EF的数量关系
2.如图2,若∠ABC=30°,∠ADB=∠BEC=60°,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明;
3.如图3,若∠ADB=∠BEC=2∠ABC,原问题中的其他条件不变,你在(1)中

得到的结论是否发生变化?请写出你的猜想并加以证明
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com