
【题目】如图,![]() 内接于
内接于![]() ,且
,且![]() 为
为![]() 的直径.
的直径.![]() 的平分线交
的平分线交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
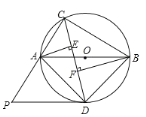
(1)求证:![]() ;
;
(2)试猜想线段![]() ,
,![]() ,
,![]() 之间有何数量关系,并加以证明;
之间有何数量关系,并加以证明;
(3)若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)见解析;(2)![]() ,证明见解析;(3)
,证明见解析;(3)![]()
【解析】
(1)连结OD,先由已知△ABD是等腰直角三角形,得DO⊥AB,再根据切线的性质得OD⊥PD,于是可得到DP∥AB;
(2)由“一线三垂直模型”易得![]() ,进而可得
,进而可得![]() .
.
(3)利用勾股定理依次可求直径AB=10,![]() ,
,![]() ,得
,得![]() ,再证明
,再证明![]() 可得
可得![]() ,
,![]() ,进而由
,进而由![]() 求得PD即可.
求得PD即可.
(1)证明:连结![]() ,如图,
,如图,
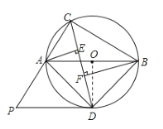
∵![]() 为
为![]() 的直径,
的直径,
∴![]() ,
,
∵![]() 的平分线交
的平分线交![]() 于点
于点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∵![]() 为
为![]() 的切线,
的切线,
∴![]() ,
,
∴![]() ;
;
(2)答:![]() ,证明如下:
,证明如下:
∵![]() 是
是![]() 的直径,
的直径,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
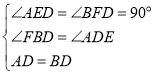
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
即![]() .
.
(3)解:在![]() 中,
中,![]() ,
,
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]()
∵![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
在![]() 中,
中,![]()
![]() ,
,
∴![]()
![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
而![]() ,
,
∴![]() ,
,
∴![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
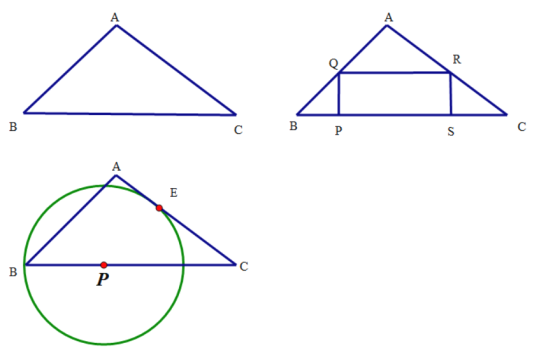
【题目】如图1,在△ABC中,∠ABC=45°,BC=7cm,AB=![]() cm。点P从点B出发沿BC方向向点C运动,当点P到点C时,停止运动
cm。点P从点B出发沿BC方向向点C运动,当点P到点C时,停止运动
(1)如图2,过点P作PQ⊥BC,PQ交AB于点Q,以PQ为一边向右侧作矩形PQRS,若点R恰好在边AC上,且满足QR=2PQ.求BP得值.
(2)以点P为圆心,BP为半径作圆.
①如图3,当⊙P与边AC相切于点E时,求BP的值;
②随着BP的变化,⊙P与△ABC三边的公共点的个数也在变化,请直接写出公共点个数与对应的BP的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
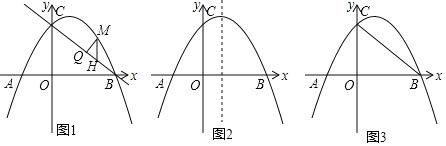
【题目】如图1,已知抛物线y=﹣![]() x+3与x轴交于A和B两点,(点A在点B的左侧),与y轴交于点C.
x+3与x轴交于A和B两点,(点A在点B的左侧),与y轴交于点C.
(1)求出直线BC的解析式.
(2)M为线段BC上方抛物线上一动点,过M作x轴的垂线交BC于H,过M作MQ⊥BC于Q,求出△MHQ周长最大值并求出此时M的坐标;当△MHQ的周长最大时在对称轴上找一点R,使|AR﹣MR|最大,求出此时R的坐标.
(3)T为线段BC上一动点,将△OCT沿边OT翻折得到△OC′T,是否存在点T使△OC′T与△OBC的重叠部分为直角三角形,若存在请求出BT的长,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
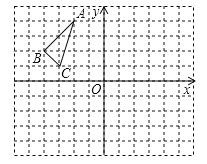
【题目】 ![]() 在平面直角坐标系中的位置如图,其中每个小正方形的边长为
在平面直角坐标系中的位置如图,其中每个小正方形的边长为![]() 个单位长度.
个单位长度.
![]() 画出
画出![]() 关于原点
关于原点![]() 的中心对称图形
的中心对称图形![]() ;
;
![]() 画出将
画出将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() .
.
![]() 在
在![]() 的条件下,求点
的条件下,求点![]() 旋转到点
旋转到点![]() 所经过的路线长(结果保留
所经过的路线长(结果保留![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
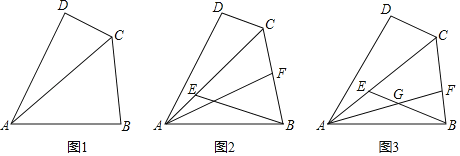
【题目】如图1,四边形ABCD中,对角线AC平分∠DCB,且AD=AB,CD<CB
(1)求证:∠B+∠D=180°;
(2)如图2,在AC上取一点E,使得BE∥CD,且BE=CE,点F在线段BC上,连接AF,且AB=AF,求证:AE=CF;
(3)如图3,在(2)的条件下,若BE与AF交于点G,BF:AB=2:7,求tan∠BGF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“分组合作学习”成为我市推动课堂教学改革,打造自主高效课堂的重要举措.某中学从全校学生中随机抽取100人作为样本,对“分组合作学习”实施前后学生的学习兴趣变化情况进行调查分析,统计如下:
分组前学生学习兴趣 分组后学生学习兴趣
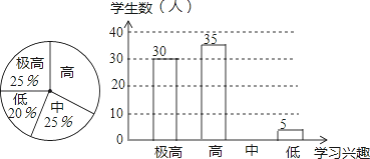
请结合图中信息解答下列问题:
(1)求出分组前学生学习兴趣为“高”的所占的百分比为 ;
(2)补全分组后学生学习兴趣的统计图;
(3)通过“分组合作学习”前后对比,请你估计全校2000名学生中学习兴趣获得提高的学生有多少人?请根据你的估计情况谈谈对“分组合作学习”这项举措的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣![]() x2+
x2+![]() x+3的图象与x轴交于点A、B(B在A右侧),与y轴交于点C.
x+3的图象与x轴交于点A、B(B在A右侧),与y轴交于点C.
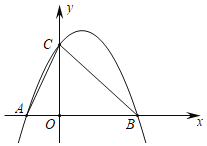
(1)求点A、B、C的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
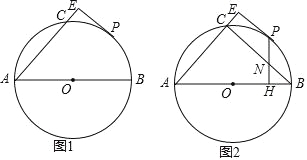
【题目】如图1,AB是⊙O的直径,AC是弦,点P是![]() 的中点,PE⊥AC交AC的延长线于E.
的中点,PE⊥AC交AC的延长线于E.
(1)求证:PE是⊙O的切线;
(2)如图2,作PH⊥AB于H,交BC于N,若NH=3,BH=4,求PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下,中学生完成数学家庭作业时,注意力指数随时间x(分钟)的变化规律如图所示(其中AB、BC为线段,CD为双曲线的一部分).
(1)分别求出线段AB和双曲线CD的函数关系式;
(2)若学生的注意力指数不低于40为高效时间,根据图中信息,求出一般情况下,完成一份数学家庭作业的高效时间是多少分钟?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com