
 抛物线y=x2-2mx+m2-4与x轴交于A,B两点(A点在B点的左侧),与y轴交于点C,抛物线的对称轴为x=1.
抛物线y=x2-2mx+m2-4与x轴交于A,B两点(A点在B点的左侧),与y轴交于点C,抛物线的对称轴为x=1.分析 (1)根据对称轴x=1可以求得m的值,即可解题;
(2)易求A、B坐标,即可求得AB长度,即可求得CD长度,即可解题;
(3)作出图形,根据图形G与线段CD有公共点,即可求得最大翻转和最小翻转,即可解题.
解答 解:(1)∵抛物线y=x2-2mx+m2-4=(x-m)2-4,其对称轴为x=1,
∴m=1.
∴该抛物线的表达式为y=x2-2x-3;
(2)当y=0时,x2-2x-3=0,解得x1=-1,x2=3,
∴抛物线与x轴的交点为A(-1,0),B(3,0).
∴AB=4.
当x=0时,y=-3,
∴抛物线与y轴的交点为C(0,-3).
∵$CD=\frac{1}{2}AB$,∴CD=2.
∵CD∥x轴,点D在点C的左侧,
∴点D的坐标为(-2,-3).
(3)作出图形,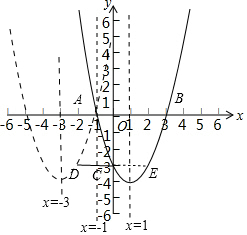
图形G与线段CD有公共点,
最小翻折为点E翻转后E1 和点C重合,此时x=1,
最大翻折为点C翻转后C1 和点D重合,此时x=-1,
∴当-1≤t≤1时,图形G与线段CD有公共点.
点评 本题考查了抛物线与坐标轴交点的计算,考查了抛物线对称轴的计算,本题中作图找到最大和最小翻转是解题的关键.


科目:初中数学 来源:2017届辽宁省九年级3月月考数学试卷(解析版) 题型:单选题
某厂生产了5000个零件,从中抽取了50个零件做质量检查,在这一问题中( )
A. 5000个零件是总体 B. 50个是样本
C. 抽取的50个零件的质量是一个样本 D. 50个零件是样本容量
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
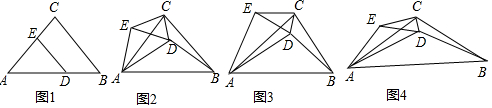
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
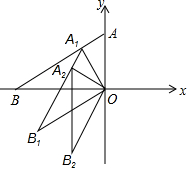 如图,点A(0,1),点B(-$\sqrt{3}$,0),作OA1⊥AB,垂足为A1,以OA1为边作Rt△A1OB1,使∠A1OB1=90°,∠B1=30°,作OA2⊥A1B1,垂足为A2,再以OA2为边作Rt△A2OB2,使∠A2OB2=90°,∠B2=30°,…,以同样的作法可得到Rt△AnOBn,则当n=2017时,点A2017的纵坐标为( )
如图,点A(0,1),点B(-$\sqrt{3}$,0),作OA1⊥AB,垂足为A1,以OA1为边作Rt△A1OB1,使∠A1OB1=90°,∠B1=30°,作OA2⊥A1B1,垂足为A2,再以OA2为边作Rt△A2OB2,使∠A2OB2=90°,∠B2=30°,…,以同样的作法可得到Rt△AnOBn,则当n=2017时,点A2017的纵坐标为( )| A. | ($\frac{\sqrt{3}}{2}$)2017 | B. | -($\frac{\sqrt{3}}{2}$)2017 | C. | ($\frac{\sqrt{3}}{2}$)2018 | D. | -($\frac{\sqrt{3}}{2}$)2018 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
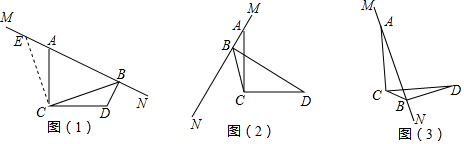
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
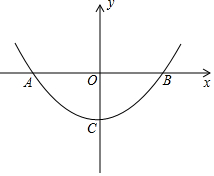 抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P在抛物线上,P(1,-3),B(4,0).
抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P在抛物线上,P(1,-3),B(4,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
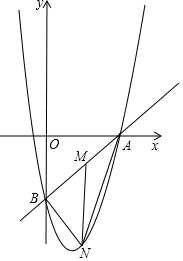 如图,直线y=$\frac{3}{4}$x-3与x轴、y轴交于A,B两点,抛物线y=x2+bx+c经过点A,B两点,M是射线BA上一个动点,MN∥y轴交抛物线于点N.
如图,直线y=$\frac{3}{4}$x-3与x轴、y轴交于A,B两点,抛物线y=x2+bx+c经过点A,B两点,M是射线BA上一个动点,MN∥y轴交抛物线于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com