
����Ŀ�����ݵ�ʽ�Ͳ���ʽ�����ʣ����Եõ�����a��b��0����a��b����a��b=0����a=b����a��b��0����a��b���������á�������Ƚ�����������������ʽֵ�Ĵ�С��
��1���ԱȽϴ���ʽ5m2��4m+2��4m2��4m��7��ֵ֮��Ĵ�С��ϵ��
��2����֪A=5m2��4�� ![]() m��
m�� ![]() ����B=7��m2��m��+3����������ǰ����ܵķ����Ƚϴ���ʽA��B�Ĵ�С��
����B=7��m2��m��+3����������ǰ����ܵķ����Ƚϴ���ʽA��B�Ĵ�С��
���𰸡�
��1���⣺5m2��4m+2����4m2��4m��7��=5m2��4m+2��4m2+4m+7=m2+9��0��
�����ʽ5m2��4m+2���ڴ���ʽ4m2��4m��7
��2���⣺��A=5m2��7m+2��B=7m2��7m+3��
��A��B=5m2��7m+2��7m2+7m��3
=��2m2��1
��m2��0
�ੁ2m2��1��0 ��A��B
����������1������2����������г�����ʽ��Ȼ��ȥ���š��ϲ�ͬ����ɣ�
�����㾫����������Ĺؼ����������ʽ�����֪ʶ�����յ�ʽ����ͬʱ���ϻ��ȥ����Ի���ԣ���Ϊ0��һ������ʽ�����ý�����ǵ�ʽ���Լ��Բ���ʽ�����ʵ����⣬�˽�1������ʽ������ͬʱ����(���ȥ)ͬһ����(��ʽ��)�����Ⱥŵķ��� ��2������ʽ������ͬʱ����(�����)ͬһ�� ���� �����Ⱥŵķ��� ���� ��3������ʽ������ͬʱ����(�����)ͬһ�� ���� ���ķ��� �ı䣮


 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������������ĺͲ�����27�������������������У� ��
A. 3�� B. 4�� C. 5�� D. 6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������쳧��������Ԥ������������һ���������������ÿ������35�������10����������������ÿ������40������ɳ�������20��.����Ԥ�������Ƕ����죿�ƻ�����������������
����Ԥ������Ϊx�죬�ƻ�����y���������������������գ����г���������x��y��ֵ.
��1����ÿ������35������Ԥ������x���ڿ�����__________�����ȼƻ�����y������__________����������������������10������ɵö�Ԫһ�η���______________________.
��2����ÿ������40������Ԥ������x���ڿ�����__________�����ȼƻ�����y__________������������������������20��������ж�Ԫһ�η���_________________________.
��3�������_________________________�������________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ����5x3+2x4y��3xy2��+��x3+3xy2+y3������6x3��x2y2+2y3�������� x��2��y����1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�����и���ǵ�λ�ã��жϴ�����ǣ� �� 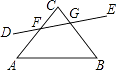
A.��C�͡�CFG��ͬ���ڽ�
B.��CGF�͡�AFG���ڴ���
C.��BGF�͡�A��ͬ���ڽ�
D.��BGF�͡�AFD��ͬλ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�ijУ300������ѧ����˯��ʱ�䣬���г�ȡ30��ѧ�����е��飬����������У�����˵����ȷ���ǣ� ��
A.300��ѧ��������
B.300����������
C.30��ѧ���dz�ȡ��һ������
D.30������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ϊ���������
A. ������һ�Ƕ�Ӧ��ȵ�����������ȫ��
B. ���� x2��2x��3��0����������ȵ�ʵ����
C. ���֮��Ϊ1��2���������������ε��ܳ�֮����1��4
D. ˳�����������ı��θ����е�õ����ı�����ƽ���ı���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com