
【题目】某商店欲购进甲、乙两种商品,已知甲的进价是乙的进价的一半,进3件甲商品和1件乙商品恰好用200元.甲、乙两种商品的售价每件分别为80元、130元,该商店决定用不少于6710元且不超过6810元购进这两种商品共100件.
(1)求这两种商品的进价.
(2)该商店有几种进货方案?哪种进货方案可获得最大利润,最大利润是多少?
【答案】(1)商品的进价为40元,乙商品的进价为80元.
(2)有三种进货方案:
方案1,甲种商品30件,乙商品70件;
方案2,甲种商品31件,乙商品69件;
方案3,甲种商品32件,乙商品68件.
方案1可获得最大利润,最大=4700.
【解析】
(1)设甲商品的进价为x元,乙商品的进价为y元,就有![]() ,3x+y=200,由这两个方程构成方程组求出其解即可.
,3x+y=200,由这两个方程构成方程组求出其解即可.
(2)设购进甲种商品m件,则购进乙种商品(100﹣m)件,根据不少于6710元且不超过6810元购进这两种商品100的货款建立不等式,求出其值就可以得出进货方案,设利润为W元,根据利润=售价﹣进价建立解析式就可以求出结论.
解:(1)设甲商品的进价为x元,乙商品的进价为y元,由题意,得
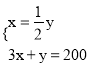 ,解得:
,解得:![]() .
.
答:商品的进价为40元,乙商品的进价为80元.
(2)设购进甲种商品m件,则购进乙种商品(100﹣m)件,由题意,得
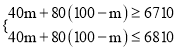 ,解得:
,解得:![]() .
.
∵m为整数,∴m=30,31,32.
∴有三种进货方案:
方案1,甲种商品30件,乙商品70件;
方案2,甲种商品31件,乙商品69件;
方案3,甲种商品32件,乙商品68件.
设利润为W元,由题意,得![]() ,
,
∵k=﹣10<0,∴W随m的增大而减小.
∴m=30时,W最大=4700.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 在数轴上对应的数为
在数轴上对应的数为![]() ,点
,点![]() 对应的数为
对应的数为![]() ,且
,且![]() ,
,![]() 满足
满足![]() .
.
(1)求点![]() 与点
与点![]() 在数轴上对应的数
在数轴上对应的数![]() 和
和![]() ;
;
(2)现动点![]() 从点
从点![]() 出发,沿数轴向右以每秒
出发,沿数轴向右以每秒![]() 个单位长度的速度运动;同时,动点
个单位长度的速度运动;同时,动点![]() 从点
从点![]() 出发,沿数轴向左以每秒
出发,沿数轴向左以每秒![]() 个单位长度的速度运动,设点
个单位长度的速度运动,设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
① 若点![]() 和点
和点![]() 相遇于点
相遇于点![]() , 求点
, 求点![]() 在数轴上表示的数;
在数轴上表示的数;
② 当点![]() 和点
和点![]() 相距
相距![]() 个单位长度时,直接写出
个单位长度时,直接写出![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上.根据图中提供的信息,有下列说法:
①食堂离小明家0.4km;
②小明从食堂到图书馆用了3min;
③图书馆在小明家和食堂之间;
④小明从图书馆回家的平均速度是0.04km/min.
其中正确的有( )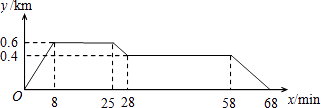
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,OA=90cm,OB=30cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学七年级同学要在清明节到烈士陵园扫墓,计划制作![]() 朵小白花学生会主席小琳先做了
朵小白花学生会主席小琳先做了![]() 天,后来好朋友小雯也加入一起做了
天,后来好朋友小雯也加入一起做了![]() 天,最后比计划多制作
天,最后比计划多制作![]() 朵小白花.已知小雯每天比小琳少制作
朵小白花.已知小雯每天比小琳少制作![]() 朵小白花.请问:小琳、小雯平均每天分别能制作多少朵小白花?
朵小白花.请问:小琳、小雯平均每天分别能制作多少朵小白花?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:菱形OBCD在平面直角坐标系中位置如图所示,点B的坐标为(2,0),∠DOB=60°.
(1)点D的坐标为 , 点C的坐标为;
(2)若点P是对角线OC上一动点,点E(0,﹣ ![]() ),求PE+PB的最小值.
),求PE+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1) 定义:直角三角形两直角边的平方和等于斜边的平方.如:直角三角形的直角边分别为3、4,则斜边的平方=32+42=25.已知:Rt△ABC中,∠C=90°,AC=8,AB=10,直接写出BC2=__________________.
(2)应用:已知正方形ABCD的边长为4,点P为AD边上的一点,AP= ![]() ,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.
,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com