
分析 设Q(1,0),连结PQ并延长到点P′,使P′Q=PQ,设P′(x,y),则x<0,y>0.过P作PM⊥x轴于点M,过P′作PN⊥x轴于点N.利用AAS证明△QP′N≌△QPM,得出QN=QM,P′N=PM,即1-x=3-1,y=2,求出x=-1,y=2,进而得到P′的坐标.
解答 解:如图,设Q(1,0),连结PA并延长到点P′,使P′Q=PQ,设P′(x,y),则x<0,y>0.
过P作PM⊥x轴于点M,过P′作PN⊥x轴于点N.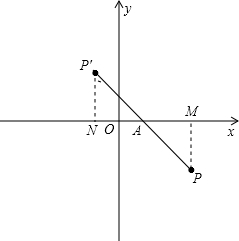
在△QP′N与△QPM中,
$\left\{\begin{array}{l}{∠QAP′=∠QMP}\\{∠NQP′=∠MQP}\\{QP′=QP}\end{array}\right.$,
∴△QP′N≌△QPM(AAS),
∴QN=QM,P′N=PM,
∴1-x=3-1,y=2,
∴x=-1,y=2,
∴P′(-1,2).
故答案为(-1,2).
点评 本题考查了坐标与图形变化-旋转,全等三角形的判定与性质,准确作出点P(3,-2)关于点(1,0)对称的点P′是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,抛物线为二次函数y=x2-4x的图象.
如图,抛物线为二次函数y=x2-4x的图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC是等腰直角三角形,DE是过点C的直线,BD⊥DE,AE⊥DE,则△BDC与△ACE通过下列变换:
如图,△ABC是等腰直角三角形,DE是过点C的直线,BD⊥DE,AE⊥DE,则△BDC与△ACE通过下列变换:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△AOB绕O点按顺时针方向旋转得到△COD,当OA⊥OC时,在这个旋转过程中:
如图,△AOB绕O点按顺时针方向旋转得到△COD,当OA⊥OC时,在这个旋转过程中:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 一块长16m,宽12m的矩形荒地上,要建一个花园,使花园所占面积为荒地面积的一半,小明的设计方案如图,设花园宽度为xm,欲求x,可列方程(16-x)(12-x)=$\frac{1}{2}$×16×12.
一块长16m,宽12m的矩形荒地上,要建一个花园,使花园所占面积为荒地面积的一半,小明的设计方案如图,设花园宽度为xm,欲求x,可列方程(16-x)(12-x)=$\frac{1}{2}$×16×12.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com