
如图,一直线AC与已知直线AB: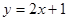 关于y轴对称。
关于y轴对称。
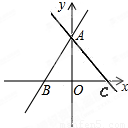
(1)求直线AC的解析式;
(2)说明两直线与x轴围成的三角形是等腰三角形。
(1)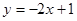 ;(2)由BO=CO,∠AOB=∠AOC=90°,再结合公共边AO即可证得△AOB≌△AOC,即可证得结论.
;(2)由BO=CO,∠AOB=∠AOC=90°,再结合公共边AO即可证得△AOB≌△AOC,即可证得结论.
【解析】
试题分析:(1)先求出直线AB: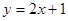 与坐标轴的交点A、B,再根据轴对称的性质即可求得点C的坐标,设直线AC的解析式为
与坐标轴的交点A、B,再根据轴对称的性质即可求得点C的坐标,设直线AC的解析式为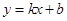 ,根据待定系数法即可求得结果;
,根据待定系数法即可求得结果;
(2)由BO=CO,∠AOB=∠AOC=90°,再结合公共边AO即可证得△AOB≌△AOC,即可证得结论.
(1)在直线AB: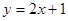 中,当
中,当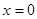 时,
时,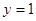 ,当
,当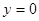 时,
时,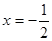
则A点坐标为(0,1),B点坐标为(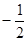 ,0)
,0)
根据轴对称的性质可得C点坐标为(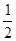 ,0)
,0)
设直线AC的解析式为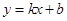
∵图象过点A(0,1),C(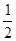 ,0)
,0)
∴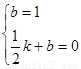 ,解得
,解得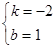
∴直线AC的解析式为 ;
;
(2)∵BO=CO,∠AOB=∠AOC=90°,AO=AO
∴△AOB≌△AOC
∴AB=AC
∴两直线与x轴围成的三角形是等腰三角形.
考点:一次函数的图象,轴对称的性质,全等三角形的判定和性质,等腰三角形的判定
点评:解题的关键是熟练掌握函数图象上的适合函数关系式,即代入关系式后能使左右两边相等.


科目:初中数学 来源: 题型:
| m | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 | 2 |
 B重合),且保持DE∥AB.以DE为边向上作正方形DEFG.
B重合),且保持DE∥AB.以DE为边向上作正方形DEFG.查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省姜堰市八年级上学期期末考试数学试卷(带解析) 题型:解答题
如图,一直线AC与已知直线AB: 关于y轴对称。
关于y轴对称。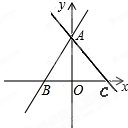
(1)求直线AC的解析式;
(2)说明两直线与x轴围成的三角形是等腰三角形。
查看答案和解析>>
科目:初中数学 来源:2011年浙江省湖州市长兴实验初中中考数学模拟试卷(解析版) 题型:解答题
 ,经过点(1,-3)、(3,-2),与x轴交于A、B两点,与y轴交于点C.D、E分别是边AC、BC上的两个动点(不与A、B重合),且保持DE∥AB.以DE为边向上作正方形DEFG.
,经过点(1,-3)、(3,-2),与x轴交于A、B两点,与y轴交于点C.D、E分别是边AC、BC上的两个动点(不与A、B重合),且保持DE∥AB.以DE为边向上作正方形DEFG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com