练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．已知$\frac{a}{b}$=$\frac{b}{c}$=$\frac{c}{a}$，求$\frac{a+b-c}{a-b+c}$的值．

    分析 可设$\frac{a}{b}$=$\frac{b}{c}$=$\frac{c}{a}$=k，可得a=bk，b=ck，c=ak，则a=bk=ck2=ak3，可得k3=1，解得k=1，依此得到a=b=c，再代入计算即可求解．

    解答 解：设$\frac{a}{b}$=$\frac{b}{c}$=$\frac{c}{a}$=k，
    则a=bk，b=ck，c=ak，
    则a=bk=ck2=ak3，
    则k3=1，
    解得k=1，
    则a=b=c，
    则$\frac{a+b-c}{a-b+c}$=$\frac{a+a-a}{a-a+a}$=1．

    点评 本题考查了比例的性质，关键是设k法的运用，难点是得到k的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．东方旅行社，某天有空客房10间，当天接待了一个旅游团，当每个房间住4人时，只有一个房间不空也不满，旅游团共有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知，如图1，已知抛物线y=a（x-h）2+k经过等边△ABD的三个顶点，点A和点B在x轴上，DH⊥AB于H，点E（-2，2）在DH上，AH=2$\sqrt{3}$，
    （1）求此抛物线的解析式；
    （2）在x轴上方的抛物线上有一动点P，过P作平行于y轴的直线PQ，交直线OE于点Q，设PQ长为d，P点的横坐标为t，求d与t的函数关系式，并直接写出t的取值范围；
    （3）在（2）问的条件下，如图2，在点P的运动过程中，连接PH交等边△ABD的边BD或AD于点M，以MH为边作等边△HMN，使点N在线段HM的上方，连接DN，当M在BD上时，∠BDN=∠DOE；或当M在DA上时，∠ADN=∠DOE；请求出满足条件的d的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．随着大陆惠及台胞政策措施的落实，台湾水果进入了大陆市场．一水果经销商购进了A、B两种台湾水果各10箱，分配给他的甲、乙两个零售店各10箱进行销售．预计每箱水果的盈利情况如表：
    A种水果（元/箱）B种水果（元/箱）
    甲店11元17元
    乙店9元13元
    （1）设甲商店有A种水果x箱，用含有x的代数式分别表示甲商店的盈利y甲、乙商店的盈利y乙；
    （2）当甲商店有多少箱A种水果时，甲、乙两商店盈利相同？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知非零向量$\overrightarrow{AB}$=2$\overrightarrow{e}$，$\overrightarrow{DC}$=3$\overrightarrow{e}$（e≠0），且|$\overrightarrow{AD}$|=|$\overrightarrow{BC}$|，则四边形ABCD是什么特殊四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

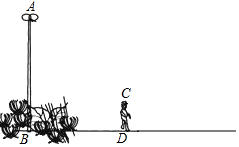    15．如图，小明同学利用灯光测一灯杆的高度．图中线段AB表示直立在花丛中的灯杆，线段CD表示小明，点A表示照明灯．
    （1）在图中画出小明在灯光照射下的影子DE．
    （2）已知小明同学身高CD=1.6m，在地面的影长DE=2m，若此时测得小明与灯杆的距离BD=13m，则旗杆高应为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，AB是⊙O的直径，AC是⊙O的弦，AD平分∠CAB交⊙O于点D，AC=6，AB=10，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．已知x=-2是关于x的方程$\frac{1}{2}$（1-2ax）=x+a的解，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．运用乘法公式计算
    （1）（3x-5）2-（2x+7）2；
    （2）（x-y+1）（x+y-1）；
    （3）（2x-y-3）2；
    （4）（x+2）2（x-2）2；
    （5）（a+2）（a-2）（a2+4）（a4+16）；
    （6）（a+2b+3c）2．

    查看答案和解析>>

    同步练习册答案