
【题目】一个圆锥的高为3![]() cm,侧面展开图是半圆,
cm,侧面展开图是半圆,
求:(1)圆锥母线与底面半径的比;
(2)锥角的大小;
(3)圆锥的全面积.
【答案】(1)2;(2)60°;(3)27π.
【解析】试题分析:(1)根据展开图是半圆,可求得母线与半径比值.
(2)利用结论(1)可知锥角大小.
(3)由(2)结论,利用特殊三角形计算出底面半径和母线长,分别求出侧面积和底面积.
试题解析:
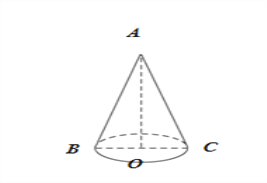
如图,AO为圆锥的高,经过AO的截面是等腰△ABC,则AB为圆锥母线l,BO为底面半径r.
(1)因圆锥的侧面展开图是半圆,所以2πr=πl,则![]() =2.
=2.
(2)因![]() =2,则有AB=2OB,∠BAO=30°,所以∠BAC=60°,即锥角为60°.
=2,则有AB=2OB,∠BAO=30°,所以∠BAC=60°,即锥角为60°.
(3)因圆锥的母线l,高h和底面半径r构成直角三角形,所以l2=h2+r2;又l=2r,h=3![]() cm,则r=3 cm,l=6 cm.
cm,则r=3 cm,l=6 cm.
所以S表=S侧+S底=πrl+πr2=3·6π+32π=27π(cm2).


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°.
(1)△ACD是直角三角形吗?为什么?
(2)小区为美化环境,欲在空地上铺草坪,已知草坪每平方米80元,试问铺满这块空地共需花费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③a-2b+4c<0;④8a+c>0.其中正确的有____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() ,且
,且![]() ,
,![]() 满足
满足![]() .过点
.过点![]() 分别作
分别作![]() 轴、
轴、![]() 轴,垂足分别是点
轴,垂足分别是点![]() 、
、![]() .
.


(1)求出点![]() 的坐标;
的坐标;
(2)点![]() 是边
是边![]() 上的一个动点(不与点
上的一个动点(不与点![]() 重合),
重合),![]() 的角平分线交射线
的角平分线交射线![]() 于点
于点![]() ,在点
,在点![]() 运动过程中,
运动过程中,![]() 的值是否变化?若不变,求出其值;若变化,说明理由.
的值是否变化?若不变,求出其值;若变化,说明理由.
(3)在四边形![]() 的边上是否存在点
的边上是否存在点![]() ,使得
,使得![]() 将四边形
将四边形![]() 分成面积比为1:4的两部分?若存在,请直接写出点
分成面积比为1:4的两部分?若存在,请直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某地,人们发现在一定温度下某种蟋蟀叫的次数与温度之间有如下的竟是关系:

(1)在这个变化过程中,自变量是 ,因变量是 ;
(2)在当地温度![]() 每增加
每增加![]() ,这种蟋蟀
,这种蟋蟀![]() 叫的次数
叫的次数![]() 是怎样变化的?
是怎样变化的?
(3)这种蟋蟀![]() 叫的次数
叫的次数![]() (次)与当地温度
(次)与当地温度![]() 之间的关系为 ;
之间的关系为 ;
(4)当这种蟋蟀![]() 叫的次数
叫的次数![]() 时,求当时该地的温度.
时,求当时该地的温度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
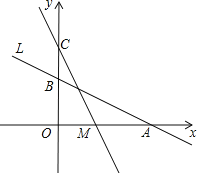
【题目】如图,直线L:y=﹣![]() x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,请直接写出此时t值和M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是![]() 的的直径,BC
的的直径,BC![]() AB于点B,连接OC交
AB于点B,连接OC交![]() 于点E,弦AD//OC,弦DF
于点E,弦AD//OC,弦DF![]() AB于点G.
AB于点G.
(1)求证:点E是![]() 的中点;
的中点;
(2)求证:CD是![]() 的切线;
的切线;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com