
【题目】温州享有“中国笔都”之称,其产品畅销全球,某制笔企业欲将n件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,各地的运费如图所示.设安排x件产品运往A地. 
(1)当n=200时,①根据信息填表:
A地 | B地 | C地 | 合计 | |
产品件数(件) | x | 2x | 200 | |
运费(元) | 30x |
②若运往B地的件数不多于运往C地的件数,总运费不超过4000元,则有哪几种运输方案?
(2)若总运费为5800元,求n的最小值.
【答案】
(1)解:①根据信息填表
A地 | B地 | C地 | 合计 | |
产品件数(件) | 200﹣3x | |||
运费 | 1600﹣24x | 50x | 56x+1600 |
②由题意,得 ![]() ,
,
解得40≤x≤42 ![]() ,
,
∵x为正整数,
∴x=40或41或42,
∴有三种方案,分别是(i)A地40件,B地80件,C地80件;
(ii)A地41件,B地77件,C地82件;
(iii)A地42件,B地74件,C地84件
(2)解:由题意,得30x+8(n﹣3x)+50x=5800,
整理,得n=725﹣7x.
∵n﹣3x≥0,
∴725﹣7x﹣3x≥0,
∴﹣10x≥﹣725,
∴x≤72.5,
又∵x≥0,
∴0≤x≤72.5且x为正整数.
∵n随x的增大而减少,
∴当x=72时,n有最小值为221
【解析】(1)①运往B地的产品件数=总件数n﹣运往A地的产品件数﹣运往B地的产品件数;运费=相应件数×一件产品的运费; ②根据运往B地的件数不多于运往C地的件数,总运费不超过4000元列出不等式组,求得正整数解的个数即可;(2)总运费=A产品的运费+B产品的运费+C产品的运费,进而根据函数的增减性及(1)中②得到的x的取值求得n的最小值即可.
【考点精析】关于本题考查的一元一次不等式组的应用,需要了解1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案才能得出正确答案.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案科目:初中数学 来源: 题型:
【题目】请在图中补全坐标系及缺失的部分,并在横线上写恰当的内容.图中各点坐标如下:A(1,0),B(6,0),C(1,3),D(6,2).线段AB上有一点M,使△ACM∽△BDM,且相似比不等于1.求出点M的坐标并证明你的结论.
M( , )
证明:∵CA⊥AB,DB⊥AB
∴∠CAM=∠DBM=度.
∵CA=AM=3,DB=BM=2
∴∠ACM=∠AMC(),∠BDM=∠BMD(同理),
∴∠ACM= ![]() (180°﹣)=45°.∠BDM=45°(同理).
(180°﹣)=45°.∠BDM=45°(同理).
∴∠ACM=∠BDM
在△ACM与△BDM中,
∠CAM=∠DBM
∴△ACM∽△BDM(如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,每个小方格都是边长为1cm的正方形,△ABC的三个顶点都在格点上,将△ABC绕点O逆时针旋转90°后得到△A′B′C′(其中A、B、C的对应点分别为A′,B′,C′,则点B在旋转过程中所经过的路线的长是cm.(结果保留π)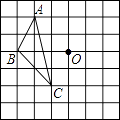
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地植物园从正门到侧门有一条小路,甲徒步从正门出发匀速走向侧门,乙与甲同时出发,骑自行车从侧门匀速前往正门到达正门后休息0.2小时,然后按原路原速匀速返回侧门,图中折线分别表示甲、乙到侧门的距离y(km)与出发时间x(h)之间的函数关系图象,根据图象信息解答下列问题:
(1)求甲到侧门的距离y与x之间的函数关系式;
(2)求甲、乙第一次相遇时到侧门的距离.
(3)求甲、乙第二次相遇的时间.
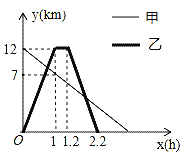
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知动点A在函数 ![]() 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x,y轴分别于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x,y轴分别于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 . 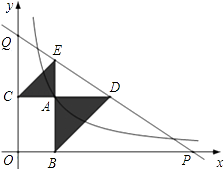
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量江两岸码头B、D之间的距离,从山坡上高度为50米的A处测得码头B的仰角∠EAB为15°,码头D的仰角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求码头B、D的距离(结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形DOE的半径为3,边长为 ![]() 的菱形OABC的顶点A,C,B分别在OD,OE,
的菱形OABC的顶点A,C,B分别在OD,OE, ![]() 上,若把扇形DOE围成一个圆锥,则此圆锥的高为( )
上,若把扇形DOE围成一个圆锥,则此圆锥的高为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.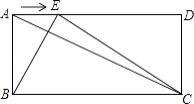
(1)若a=5,sin∠ACB= ![]() ,求b.
,求b.
(2)若a=5,b=10当BE⊥AC时,求出此时AE的长.
(3)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,AB=6,BC=8,E,F分别是AB,BC的中点,AF与DE相交于I,与BD相交于H,则四边形BEIH的面积为( )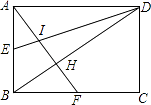
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com