
【题目】探究题:已知:如图,![]() ,
,![]() .求证:
.求证:![]() .
.
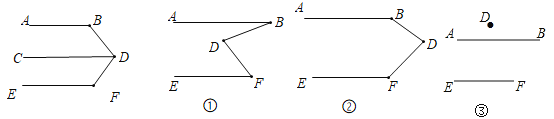
老师要求学生在完成这道教材上的题目证明后,尝试对图形进行变形,继续做拓展探究,看看有什么新发现?
(1)小颖首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小颖用到的平行线性质可能是 .
(2)接下来,小颖用《几何画板》对图形进行了变式,她先画了两条平行线![]() ,然后在平行线间画了一点
,然后在平行线间画了一点![]() ,连接
,连接![]() 后,用鼠标拖动点
后,用鼠标拖动点![]() ,分别得到了图
,分别得到了图![]()
![]() ,小颖发现图
,小颖发现图![]() 正是上面题目的原型,于是她由上题的结论猜想到图
正是上面题目的原型,于是她由上题的结论猜想到图![]() 和
和![]() 图中的与
图中的与![]() 之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
请你在小颖操作探究的基础上,继续完成下面的问题:
(ⅰ)猜想图![]() 中
中![]() 与
与![]() 之间的数量关系并加以证明;
之间的数量关系并加以证明;
(ⅱ)补全图![]() ,直接写出
,直接写出![]() 与
与![]() 之间的数量关系: .
之间的数量关系: .
【答案】(1)两直线平行同旁内角互补;(2)(ⅰ)![]() ,见解析;(ⅱ)见解析,
,见解析;(ⅱ)见解析,![]() .
.
【解析】
(1)根据两直线平行同旁内角互补即可解决问题;
(2)(ⅰ)猜想∠BDF=∠B+∠F.过点D作CD∥AB.利用平行线的性质即可解决问题;
(ⅱ)∠BDF与∠F之间的数量关系是∠F=∠B+∠BDF.利用平行线的性质已经三角形的外角的性质即可解决问题;
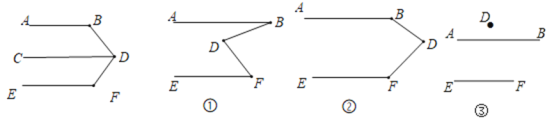
解:(1)∵AB//CD,
∴∠B+∠BDC=180°(两直线平行,同旁内角互补),
∵CD//EF(已知),
∴∠CDF+∠DFE=180°(两直线平行,同旁内角互补),
∴∠B+∠BDF+∠F=∠B+∠BDC+∠CDF+∠DFE=360°.
故答案为:两直线平行同旁内角互补.
(2)(ⅰ)猜想![]()
证明:过点![]() 作
作![]() ,
,

![]()
![]() ,
,
![]()
![]()
![]()
![]()
(ⅱ)补全图形如图所示:∠B、∠BDF与∠F之间的数量关系是∠F=∠B+∠BDF.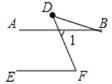
理由:∵AB∥EF,
∴∠1=∠F,
∵∠1=∠B+∠D,
∴∠F=∠B+∠BDF.
故答案为∠F=∠B+∠BDF.


科目:初中数学 来源: 题型:
【题目】观察下面三行数:
-1、2、-4、8、-16、32、-64、……①
0、3、-3、9、-15、33、-63、……②
1、-5、7、-17、31、-65、127、……③
(1) 第①行的第8个数是___________,第①行第n个数是___________(用n的式子表示)
(2) 取第①、②、③行的第10个数分别记为a、b、c,求a-b+c的值
(3) 取每行数的第n个数,这三个数中任意两数之差的最大值为6146,则n=__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某班“讲故事”比赛中有一个抽奖活动,活动规则是:只有进入最后决赛的甲、乙、丙三位同学,每人才能获得一次抽奖机会.在如图所示的翻奖牌正面的4个数字中选一个数字,选中后就可以得到该数字后面的相应奖品:前面的人选中的数字,后面的人就不能再选择数字了.
(1)请用树状图(或列表)的方法求甲、乙二人得到的奖品都是计算器的概率.
(2)有的同学认为,如果甲先翻奖牌,那么他得到篮球的概率会大些,这种说法正确吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,△DCE是△ABC绕着点C顺时针方向旋转得到的,此时B、C、E在同一直线上.
(1)旋转角的大小;
(2)若AB=10,AC=8,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,公路 MN 和公路 PQ 在点 P 处交会,且∠QPN=30°.点 A 处有一所中学,AP=160m,一辆拖拉机从 P 沿公路 MN 前行,假设拖拉机行驶时周围 100m 以内会受到噪声影响,那么该所中学是否会受到噪声影响,请说明理由,若受影响,已知拖拉机的速度为 18km/h,那么学校受影响的时间为多长?
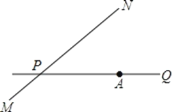
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.

(1)若AB=4,求弧CD的长.
(2)若弧BC=弧AD,AD=AP. 求证:PD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度,则点B所对应的数是_____.
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.
(3)在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为6×6的正方形网格,每个小正方形的顶点均为格点,在图中已标出线段AB,A,B均为格点,按要求完成下列问题.
(1)以AB为对角线画一个面积最小的菱形AEBF,且E,F为格点;
(2)在(1)中该菱形的边长是 ,面积是 ;
(3)以AB为对角线画一个菱形AEBF,且E,F为格点,则可画 个菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)从A地到B地,某甲走直径AB上方的半圆途径;乙先走直径AC上方半圆的途径,再走直径CB下方半圆的途径,如图1,已知AB=40米,AC=30米,计算个人所走的路程,并比较两人所走路程的远近;
(2)如果甲.乙走的路程图改成图2,两人走的路程远近相同吗?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com