
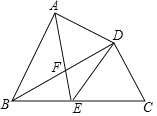
【题目】如图,在四边形ABCD中,对角线BD平分![]() ,
,![]() ,E为BC的中点,AE与BD相交于点F,若
,E为BC的中点,AE与BD相交于点F,若![]() ,则BF的长为( )
,则BF的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
连接DE,结合直角三角形性质得出CD=DE=1,BC=2,BD=![]() ,AB=
,AB=![]() ,然后利用角平分线性质证明出∠BDE=∠ABD,从而得出△AFB∽EFD,根据相似三角形对应边成比例进一步求解即可.
,然后利用角平分线性质证明出∠BDE=∠ABD,从而得出△AFB∽EFD,根据相似三角形对应边成比例进一步求解即可.
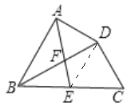
如图,连接DE,
∵![]() ,
,
∴△BDC是直角三角形,且∠C=60°,
∵E为BC的中点,
∴DE=BE=EC,
∴∠BDE=∠DBC=30°,
∴∠EDC=60°,
∴△DEC是等边三角形,
∴DE=EC=CD=1,
∴BC=2,
∴BD=![]() ,
,
∵BD平分![]() ,
,
∴∠ABD=∠DBC=30°,
∴AB=BD×cos30°=![]()
∵∠BDE=∠DBC=30°,
∴∠BDE=∠ABD,
∴△ABF∽△EDF,
∴![]() =
=![]() ,
,
∴BF=![]() ,
,
所以答案为C选项.


科目:初中数学 来源: 题型:
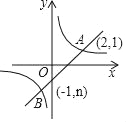
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A、B两点.
的图象交于A、B两点.
(1)利用图中的条件,求反比例函数和一次函数的解析式.
(2)求△AOB的面积.
(3)根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,点A(0,8),点B(m,0),且m>0.把△AOB绕点A逆时针旋转90°,得△ACD,点O,B旋转后的对应点为C,D,
(1)点C的坐标为 ;
(2)①设△BCD的面积为S,用含m的式子表示S,并写出m的取值范围;
②当S=6时,求点B的坐标(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用热气球探测器测量大楼AB的高度.从热气球P处测得大楼顶部B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离地面的高度为120m.试求大楼AB的高度(精确到0.1m).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注,“六一”期间,记者随机调查了某校若干名初三学生和家长对中学生带手机现象的看法,统计整理并制作了如下两幅统计图.

![]() 求这次调查的家长人数,并补全条形图;
求这次调查的家长人数,并补全条形图;
![]() 求扇形图中表示家长“赞成”的圆心角的度数;
求扇形图中表示家长“赞成”的圆心角的度数;
![]() 若某地区共有初三学生
若某地区共有初三学生![]() 名,请估计在这些学生中,对中学生带手机现象持“无所谓”态度的人数约是多少?
名,请估计在这些学生中,对中学生带手机现象持“无所谓”态度的人数约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系内,![]() 的三个顶点的分别为
的三个顶点的分别为![]() ,
,![]() ,
,![]() (正方形网格中每个小正方形的边长是一个单位长度).
(正方形网格中每个小正方形的边长是一个单位长度).

(1)在网格内画出![]() 向下平移2个单位长度得到的
向下平移2个单位长度得到的![]() ,点
,点![]() 的坐标是________;
的坐标是________;
(2)以点![]() 为位似中心,在网格内画出
为位似中心,在网格内画出![]() ,使
,使![]() 与
与![]() 位似,且位似比为
位似,且位似比为![]() ,点
,点![]() 的坐标是________;
的坐标是________;
(3)![]() 的面积是________平方单位.
的面积是________平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
普通消费:35元/次;
白金卡消费:购卡280元/张,凭卡免费消费10次再送2次;
钻石卡消费:购卡560元/张,凭卡每次消费不再收费.
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用.
(1)李叔叔每年去该健身中心健身6次,他应选择哪种消费方式更合算?
(2)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式;
(3)王阿姨每年去该健身中心健身至少18次,请通过计算帮助王阿姨选择最合算的消费方式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 地和
地和![]() 地之间有一条笔直的公路,一天,甲车从
地之间有一条笔直的公路,一天,甲车从![]() 地去
地去![]() 地,乙车从
地,乙车从![]() 地去
地去![]() 地,乙先出发,若甲、乙之间的距离为
地,乙先出发,若甲、乙之间的距离为![]() 千米,行驶时间为
千米,行驶时间为![]() 小时,
小时,![]() 与
与![]() 之间的函数关系如图所示,则下列说法错误的是 ( )
之间的函数关系如图所示,则下列说法错误的是 ( )

A.![]() 两地间距离为100千米B.甲车的速度是80千米/时
两地间距离为100千米B.甲车的速度是80千米/时
C.甲到![]() 地比乙车到
地比乙车到![]() 地早
地早![]() 小时D.甲出发0.5小时后与乙车相遇
小时D.甲出发0.5小时后与乙车相遇
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若![]() ,则称
,则称![]() 与
与![]() 是关于
是关于![]() 的关联数.例如:若
的关联数.例如:若![]() ,则称
,则称![]() 与
与![]() 是关于2的关联数;
是关于2的关联数;
(1)若3与![]() 是关于5的关联数,求
是关于5的关联数,求![]() 的值
的值
(2)若![]() 与
与![]() 是关于4的关联数,求
是关于4的关联数,求![]() 的值.
的值.
(3)若![]() 与
与![]() 是关于
是关于![]() 的关联数,
的关联数, ![]() ,
,![]() 的值与
的值与![]() 无关,求
无关,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com