
| (1)(-2)+(-7); | (2)-32-5; | (3)(-30.5)×0.2; |
| (4)12-(-18)+(-7)-15; | (5)(-$\frac{3}{4}$)×(-1$\frac{1}{2}$)×0÷(-2$\frac{1}{4}$); | (6)-9×(-11)÷3÷(-3); |
| (7)-18÷2$\frac{1}{4}$-$\frac{4}{9}$÷(-$\frac{2}{3}$); | (8)($\frac{9}{10}$-$\frac{2}{15}$+$\frac{1}{6}$)×30; | (9)1-3.9÷[1-$\frac{3}{4}$-(-0.5)]. |
分析 (1)原式利用同号两数相加的法则计算即可得到结果;
(2)原式利用减法法则变形,计算即可得到结果;
(3)原式利用乘法法则计算即可得到结果;
(4)原式利用减法法则变形,计算即可得到结果;
(5)原式利用0乘除任何数(除时0除外)结果为0即可得到结果;
(6)原式先计算乘除运算,再计算加减运算即可得到结果;
(7)原式先计算除法运算,再计算加减运算即可得到结果;
(8)原式利用乘法分配律计算即可得到结果;
(9)原式先计算除法运算,再计算加减运算即可得到结果.
解答 解:(1)原式=-9;
(2)原式=(-32)+(-5)=-37;
(3)原式=-6.1;
(4)原式=12+18-7-15=30-22=8;
(5)原式=0;
(6)原式=99÷3÷(-3)=-11;
(7)原式=18×$\frac{4}{9}$+$\frac{4}{9}$×$\frac{3}{2}$=-8+$\frac{2}{3}$=-7$\frac{1}{3}$;
(8)原式=27-4+5=28;
(9)原式=1-3.9×$\frac{4}{3}$=1-4.2=-3.2.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:选择题
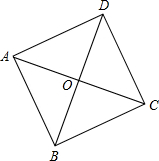 如图,在?ABCD中,AC⊥BD于点O,若增加一个条件,使得四边形ABCD是正方形,则下列条件中,不正确的是( )
如图,在?ABCD中,AC⊥BD于点O,若增加一个条件,使得四边形ABCD是正方形,则下列条件中,不正确的是( )| A. | AC=BD | B. | AB=BC | C. | ∠ABC=90° | D. | AO=BO |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )
如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )| A. | $\frac{2π}{3}$-$\sqrt{3}$ | B. | $\frac{2π}{3}$-$\frac{\sqrt{3}}{2}$ | C. | π-$\frac{\sqrt{3}}{2}$ | D. | π-$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,A($\sqrt{3}$,0),B($\sqrt{3}$,1),将△OAB绕点O逆时针旋转至△OA′B′,使点B的对应点B′,落在y轴的正半轴上.
如图,在平面直角坐标系中,A($\sqrt{3}$,0),B($\sqrt{3}$,1),将△OAB绕点O逆时针旋转至△OA′B′,使点B的对应点B′,落在y轴的正半轴上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com