
【题目】如图,在矩形ABCD中,AB=5,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为E,边CD′与⊙O相交于点F,则CF的长为
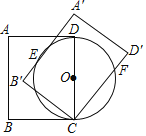
A. 2 B. 3 C. 4 D. 5
【答案】C
【解析】
连接OE,延长EO交CD于点G,作OH⊥B′C,由旋转性质知∠B′=∠B′CD′=90°、AB=CD=5、BC=B′C=4,从而得出四边形OEB′H和四边形EB′CG都是矩形且OE=OD=OC=2.5,继而求得CG=B′E=OH=![]() ,根据垂径定理可得CF的长.
,根据垂径定理可得CF的长.
连接OE,延长EO交CD于点G,作OH⊥B′C于点H,
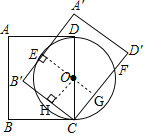
则∠OEB′=∠OHB′=90°,
∵矩形ABCD绕点C旋转所得矩形为A′B′C′D′,
∴∠B′=∠B′CD′=90°,AB=CD=5、BC=B′C=4,
∴四边形OEB′H和四边形EB′CG都是矩形,OE=OD=OC=2.5,
∴B′H=OE=2.5,
∴CH=B′C-B′H=1.5,
∴CG=B′E=OH=![]() ,
,
∵四边形EB′CG是矩形,
∴∠OGC=90°,即OG⊥CD′,
∴CF=2CG=4,
故选C.


科目:初中数学 来源: 题型:
【题目】(1)如图,用尺规作图的方法作出![]() 的角平分线
的角平分线![]() . (保留作图痕迹,不要求写出作法)
. (保留作图痕迹,不要求写出作法)
(2)在(1)的基础上证明命题“全等三角形的对应角角平分线相等”是真命题.请填空并证明.
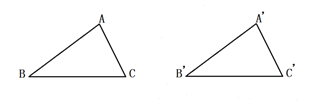
已知:如图,__________________,![]() 和
和![]() 分别是
分别是![]() 和
和![]() 的平分线.
的平分线.
求证:______________________________.
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长度为_____
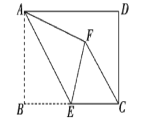
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“金源”食品加工厂需要一批食品包装盒,供应这种包装盒有两种方案可供选择:
方案一:从包装盒加工厂直接购买,购买所需的费用![]() (元)与包装盒个数
(元)与包装盒个数![]() (个)满足图中的射线
(个)满足图中的射线![]() 所示的函数关系;
所示的函数关系;
方案二:租赁机器自己加工,所需费用![]() (元)(包括租赁机器的费用和生产包装盒的费用)与包装盒个数
(元)(包括租赁机器的费用和生产包装盒的费用)与包装盒个数![]() (个)满足图中射线
(个)满足图中射线![]() 所示的函数关系.
所示的函数关系.
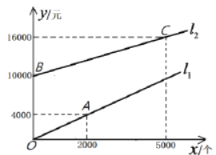
根据图象解答下列问题:
(1)点![]() 的坐标是_____________,方案一中每个包装盒的价格是___________元,射线
的坐标是_____________,方案一中每个包装盒的价格是___________元,射线![]() 所表示的函数关系式是_____________.
所表示的函数关系式是_____________.
(2)求出方案二中的![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)你认为选择哪种方案更省钱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
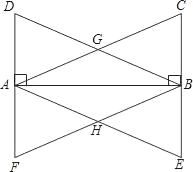
【题目】在Rt△ABC与Rt△ABD中,∠ABC=∠BAD=90°,AC=BD,AC,BD相交于点G,过点A作AE∥DB交CB的延长线于点E,过点B作BF∥CA交DA的延长线于点F,AE,BF相交于点H.
(1)证明:△ABD≌△BAC.
(2)四边形AHBG是什么样的四边形,请猜想并证明.
(3)若使四边形AHBG是正方形,还需在Rt△ABC添加一个什么条件?请添加条件并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
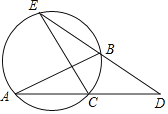
【题目】如图,A、B、C是⊙O上的点,D是弦AC的延长线一点,且BA=BD,DB的延长线交⊙O于E.
(1)求证:CD=CE;
(2)若C为AD的中点,求证:AB是⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
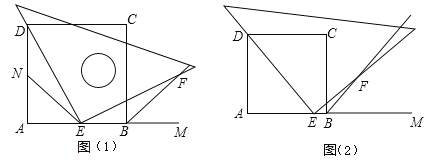
【题目】如图所示,四边形![]() 是正方形,
是正方形, ![]() 是
是![]() 延长线上一点.直角三角尺的一条直角边经过点
延长线上一点.直角三角尺的一条直角边经过点![]() ,且直角顶点
,且直角顶点![]() 在
在![]() 边上滑动(点
边上滑动(点![]() 不与点
不与点![]() 重合),另一直角边与
重合),另一直角边与![]() 的平分线
的平分线![]() 相交于点
相交于点![]() .
.
(1)求证: ![]() ;
;
(2)如图(1),当点![]() 在
在![]() 边的中点位置时,猜想
边的中点位置时,猜想![]() 与
与![]() 的数量关系,并证明你的猜想;
的数量关系,并证明你的猜想;
(3)如图(2),当点![]() 在
在![]() 边(除两端点)上的任意位置时,猜想此时
边(除两端点)上的任意位置时,猜想此时![]() 与
与![]() 有怎样的数量关系,并证明你的猜想.
有怎样的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE=CF,AB∥DE,添加下列哪个条件不能证明△ABC≌△DEF的是( )
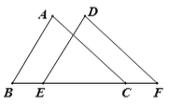
A. AB=DE B. ∠A=D C. AC=DF D. AC∥DF
查看答案和解析>>
科目:初中数学 来源: 题型:
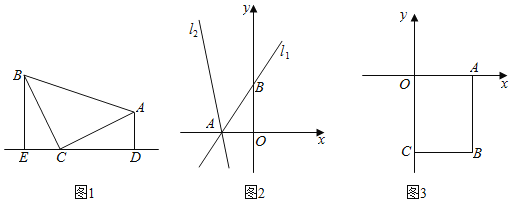
【题目】[建立模型]
(1)如图1.等腰![]() 中,
中, ![]() ,
, ![]() ,直线
,直线![]() 经过点
经过点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,求证:
,求证: ![]() ;
;
[模型应用]
(2)如图2.已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,将直线
,将直线![]() 绕点
绕点![]() 逆时针旋转45'°至直线
逆时针旋转45'°至直线![]() ,求直线
,求直线![]() 的函数表达式:
的函数表达式:
(3)如图3,平面直角坐标系内有一点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,BC⊥y
,BC⊥y![]() 轴于点
轴于点![]() ,点
,点![]() 是线段
是线段![]() 上的动点,点
上的动点,点![]() 是直线
是直线![]() 上的动点且在第四象限内.试探究
上的动点且在第四象限内.试探究![]() 能否成为等腰直角三角形?若能,求出点
能否成为等腰直角三角形?若能,求出点![]() 的坐标,若不能,请说明理由.
的坐标,若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com