
【题目】如图,在梯形ABCD中,AD//BC,AC与BD相交于点O,点E在线段OB上,AE的延长线与BC相交于点F,OD2 = OB·OE.
(1)求证:四边形AFCD是平行四边形;
(2)如果BC=BD,AE·AF=AD·BF,求证:△ABE∽△ACD.

【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)由题意,得到![]() ,然后由AD∥BC,得到
,然后由AD∥BC,得到![]() ,则
,则![]() ,即可得到AF//CD,即可得到结论;
,即可得到AF//CD,即可得到结论;
(2)先证明∠AED=∠BCD,得到∠AEB=∠ADC,然后证明得到![]() ,即可得到△ABE∽△ADC.
,即可得到△ABE∽△ADC.
证明:(1)∵OD2 =OE · OB,
∴![]() .
.
∵AD//BC,
∴![]() .
.
∴![]() .
.
∴ AF//CD.
∴四边形AFCD是平行四边形.
(2)∵AF//CD,
∴∠AED=∠BDC,![]() .
.
∵BC=BD,
∴BE=BF,∠BDC=∠BCD
∴∠AED=∠BCD.
∵∠AEB=180°![]() ∠AED,∠ADC=180°
∠AED,∠ADC=180°![]() ∠BCD,
∠BCD,
∴∠AEB=∠ADC.
∵AE·AF=AD·BF,
∴![]() .
.
∵四边形AFCD是平行四边形,
∴AF=CD.
∴![]() .
.
∴△ABE∽△ADC.


科目:初中数学 来源: 题型:
【题目】某商场将进货单价为30元的商品以每个40元的价格售出时,平均每月能售出600个,调查表明:这种商品的售价每上涨1元,其销售量就减少10个.
(1)为了使平均每月有10000元的销售利润且尽快售出,这种商品的售价应定为每个多少元?
(2)当该商品的售价为每个多少元时,商场销售该商品的平均月利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数![]() 的图象与
的图象与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,且过点
,且过点![]() .
.
(1)求二次函数表达式;
(2)若点![]() 为抛物线上第一象限内的点,且
为抛物线上第一象限内的点,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在抛物线上(![]() 下方)是否存在点
下方)是否存在点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 到
到![]() 轴的距离;若不存在,请说明理由.
轴的距离;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
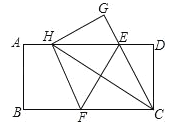
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2![]() .
.
以上结论中,你认为正确的有 .(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
材料1 若一元二次方程ax2+bx+c=0(a≠0)的两个根为x1,x2则x1+x2=﹣![]() ,x1x2=
,x1x2=![]() .
.
材料2 已知实数m,n满足m2﹣m﹣1=0,n2﹣n﹣1=0,且m≠n,求![]() 的值.
的值.
解:由题知m,n是方程x2﹣x﹣1=0的两个不相等的实数根,根据材料1得m+n=1,mn=﹣1,所以![]() =﹣3.
=﹣3.
根据上述材料解决以下问题:
(1)材料理解:一元二次方程5x2+10x﹣1=0的两个根为x1,x2,则x1+x2= ,x1x2= .
(2)类比探究:已知实数m,n满足7m2﹣7m﹣1=0,7n2﹣7n﹣1=0,且m≠n,求m2n+mn2的值:
(3)思维拓展:已知实数s、t分别满足19s2+99s+1=0,t2+99t+19=0,且st≠1.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() .顶点为
.顶点为![]() 的抛物线经过点
的抛物线经过点![]() .
.
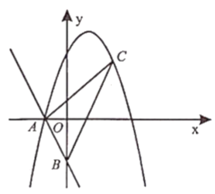
(1)求抛物线的解析式;
(2)点![]() 为第一象限抛物线上一动点.设点
为第一象限抛物线上一动点.设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() .当
.当![]() 为何值时,
为何值时,![]() 的值最大,并求
的值最大,并求![]() 的最大值;
的最大值;
(3)在(2)的结论下,若点![]() 在
在![]() 轴上,
轴上,![]() 为直角三角形,请直接写出点
为直角三角形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC,∠ABC=90°,AB=BC=2,现将Rt△ABC绕点A逆时针旋转30°得到△AED,则图中阴影部分的面积是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视举办的《主持人大赛》受到广泛的关注.某中学学生会就《主持人大赛》节目的喜爱程度,在校内对部分学生进行了问卷调查,并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级,分别记作![]() 、
、![]() 、
、![]() 、
、![]() .根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中所给信息解答下列问题:
.根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中所给信息解答下列问题:
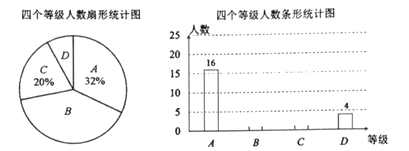
(1)本次被调查对象共有 人;扇形统计图中被调查者“比较喜欢”等级所对应圆心角的度数为 .
(2)将条形统计图补充完整,并标明数据;
(3)若选“不太喜欢”的人中有两个女生和两个男生,从选“不太喜欢”的人中挑选两个学生了解不太喜欢的原因,请用列举法(画树状图或列表),求所选取的这两名学生恰好是一男一女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com