
【题目】我们都知道连接多边形任意不相邻的两点的线段成为多边形的对角线,也都知道四边形的对角线有2条,五边形的对角线有5条
(1)六边形的对角线有 条,七边形的对角线有 条;
(2)多边形的对角线可以共有20条吗?如果可以,求出多边形的边数,如果不可以,请说明理由.
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:初中数学 来源: 题型:
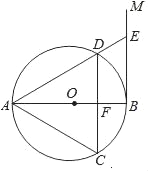
【题目】如图,AB是⊙O的直径,过点B作BM⊥AB,弦CD∥BM,交AB于点F,且DA=DC,连接AC,AD,延长AD交BM于点E.
(1)求证:△ACD是等边三角形;
(2)若AC=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京沈高速铁路赤峰至喀左段正在建设中,甲、乙两个工程队计划参与一项工程建设,甲队单独施工30天完成该项工程的![]() ,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若甲队参与该项工程施工的时间不超过36天,则乙队至少施工多少天才能完成该项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪和小明沿同一条路同时从学校出发到学校图书馆查阅资料,学校与图书馆的路程是![]() 千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达图书馆,图中折线
千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达图书馆,图中折线![]() 和线段
和线段![]() 分别表示两人离学校的路程
分别表示两人离学校的路程![]() (千米)与所经过的时间
(千米)与所经过的时间![]() (分钟)之间的函数关系,请根据图象回答下列问题:
(分钟)之间的函数关系,请根据图象回答下列问题:
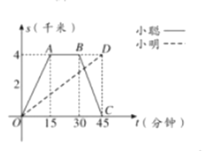
(1)小聪在图书馆查阅资料的时间为 分钟,小聪返回学校的速度为 千米/分钟;
(2)请你求出小明离开学校的路程![]() (千米)与所经过的时间
(千米)与所经过的时间![]() (分钟)之间的函数关系;
(分钟)之间的函数关系;
(3)求线段![]() 的函数关系式;
的函数关系式;
(4)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
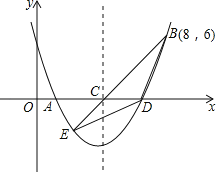
【题目】如图,二次函数y=![]() x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
(1)求二次函数的解析式.
(2)求函数图象的顶点坐标及D点的坐标.
(3)该二次函数的对称轴交x轴于C点.连接BC,并延长BC交抛物线于E点,连接BD,DE,求△BDE的面积.
(4)抛物线上有一个动点P,与A,D两点构成△ADP,是否存在S△ADP=![]() S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.
S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从宁海县到某市,可乘坐普通列车或高铁,已知高铁的行驶路程与普通列车的行驶路程之和是920千米,而普通列车的行驶路程是高铁的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若高铁的平均速度(千米/时)是普通列车的平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题发现
如图,![]() 中,
中,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() 经过点
经过点![]() ,与
,与![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() ,且
,且![]() .
.

求证:![]() 的周长等于
的周长等于![]() .
.
(1)小明做完该题后,发现![]() 、
、![]() 、
、![]() 存在特定的数量关系,请你直接写出这个数量关系;
存在特定的数量关系,请你直接写出这个数量关系;
拓广探索
(2)如图1,将题中“![]() 平分
平分![]() ”改为“
”改为“![]() 平分
平分![]() 的外角
的外角![]() ”,其他条件不变,请判断
”,其他条件不变,请判断![]() 、
、![]() 、
、![]() 的数量关系,并证明这个数量关系;
的数量关系,并证明这个数量关系;

(3)如图2,将题中“![]() 平分
平分![]() ,
,![]() 平分
平分![]() ”改为“
”改为“![]() 平分
平分![]() 的外角,
的外角,![]() 平分
平分![]() 的外角”,其他条件不变,请直接写出
的外角”,其他条件不变,请直接写出![]() 、
、![]() 、
、![]() 的数量关系.
的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在平行四边形ABCD中,AB=3cm,BC=5cm,AC⊥AB.△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿着CB方向匀速移动,速度为1cm/s;当△PNM停止平移时,点Q也停止移动,如图②.设移动时间为t(s)(0<t<4).连接PQ、MQ、MC.解答下列问题:

(1)当t为何值时,PQ∥AB?
(2)当t=3时,求△QMC的面积;
(3)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AE是△ABC的角平分线;ED平分∠AEB交AB于点D;∠CAE=∠B.
(1)如果AC=3.5 cm,求AB的长度;
(2)猜想:ED与AB的位置关系,并证明你的猜想。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com