
【题目】已知![]() 是一张直角三角形纸片,其中
是一张直角三角形纸片,其中![]() ,
,![]() ,小亮将它绕点
,小亮将它绕点![]() 逆时针旋转后
逆时针旋转后![]() 得到
得到![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() .
.

(1)如图1,当![]() 时,
时,![]() 所在直线与线段
所在直线与线段![]() 有怎样的位置关系?请说明理由.
有怎样的位置关系?请说明理由.
(2)如图2,当![]() ,求
,求![]() 为等腰三角形时的度数.
为等腰三角形时的度数.
【答案】(1)BD与FM互相垂直,理由见解析;(2)β的度数为30°或75°或120°.
【解析】
(1)由题意设直线BD与FM相交于点N,即可根据旋转的性质判断直线BD与线段MF垂直;
(2)根据旋转的性质得∠MAD=β,分类讨论:当KA=KD时,根据等腰三角形的性质得∠KAD=∠D=30°,即β=30°;当DK=DA时,根据等腰三角形的性质得∠DKA=∠DAK,然后根据三角形内角和可计算出∠DAK=75°,即β=75°;当AK=AD时,根据等腰三角形的性质得∠AKD=∠D=30°,然后根据三角形内角和可计算出∠KAD=120°,即β=120°.
解:(1)BD与FM互相垂直,理由如下
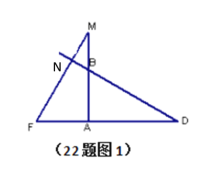
设此时直线BD与FM相交于点N
∵∠DAB=90°,∠D=30°
∴∠ABD=90°-∠D=60°,
∴∠NBM=∠ABD=60°
由旋转的性质得△ADB≌△AMF,∴∠D=∠M=30°
∴∠MNB=180°-∠M-∠NBM=180°-30°- 60°= 90°
∴BD与FM互相垂直
(2)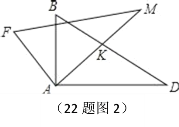
当KA=KD时,则∠KAD=∠D=30°,即β=30°;
当DK=DA时,则∠DKA=∠DAK,
∵∠D=30°,∴∠DAK=(180°﹣30°)÷2=75°,即β=75°;
当AK=AD时,则∠AKD=∠D=30°,
∴∠KAD=180°﹣30°﹣30°=120°,即β=120°,
综上所述,β的度数为30°或75°或120°.


科目:初中数学 来源: 题型:
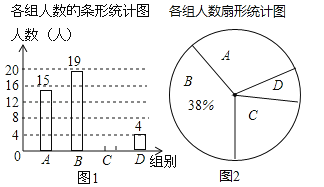
【题目】小明随机调查了若干市民租用共享单车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如下统计图(A:0<t≤10,B:10<t≤20,C:20<t≤30,D:t>30),根据图中信息,解答下列问题:
(1)这项被调查的总人数是多少人?
(2)试求表示A组的扇形统计图的圆心角的度数,补全条形统计图;
(3)如果小明想从D组的甲、乙、丙、丁四人中随机选择两人了解平时租用共享单车情况,请用列表或画树状图的方法求出恰好选中甲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文化是一个国家、一个民族的灵魂,近年来,央视推出《中国诗词大会》、《中国成语大会》、《朗读者》、《经曲咏流传》等一系列文化栏目.为了解学生对这些栏目的喜爱情况,某学校组织学生会成员随机抽取了部分学生进行调查,被调查的学生必须从《经曲咏流传》(记为A)、《中国诗词大会》(记为B)、《中国成语大会》(记为C)、《朗读者》(记为D)中选择自己最喜爱的一个栏目,也可以不选以上四类而写出一个自己最喜爱的其他文化栏目(这时记为E).根据调查结果绘制成如图所示的两幅不完整的统计图.
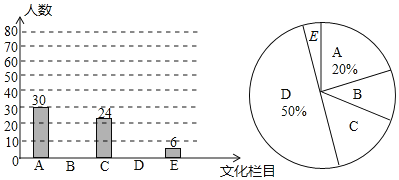
请根据图中信息解答下列问题:
(1)在这项调查中,共调查了 名学生;
(2)最喜爱《朗读者》的学生有 名;
(3)扇形统计图中“B”所在扇形圆心角的度数为 ;
(4)选择“E”的学生中有2名女生,其余为男生,现从选择“E”的学生中随机选出两名学生参加座谈,请直接写出:刚好选到一名男生和一名女生的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.一颗质地均匀的骰子已连续抛掷了2000次,其中抛掷出5点的次数最少,则第2001次一定抛掷出5点
B.抛掷一枚图钉,钉尖触地和钉尖朝上的概率不相等
C.明天降雨的概率是80%,表示明天有80%的时间降雨
D.某种彩票中奖的概率是1%,因此买100张该种彩票一定会中奖
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,B,C,D三点在![]() 上,
上,![]() ,PA是钝角△ABC的高线,PA的延长线与线段CD交于点E.
,PA是钝角△ABC的高线,PA的延长线与线段CD交于点E.
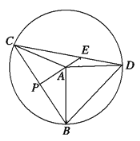
(1)请在图中找出一个与∠CAP相等的角,这个角是 ;
(2)用等式表示线段AC,EC,ED之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=1,BC=2,点E在边BC上,将△ABE沿AE折叠,点B恰好落在对角线AC上的点B′处.则线段BE的长为_____.
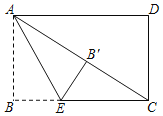
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件
B.审查书稿中有哪些学科性错误适合用抽样调查法
C.甲乙两人在相同条件下各射击10次,他们的成绩的平均数相同,方差分别是![]() =0.4,
=0.4,![]() =0.6,则甲的射击成绩较稳定
=0.6,则甲的射击成绩较稳定
D.掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区要在一块一边靠墙的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为32m的栅栏围成(如图所示).如果墙长16m,满足条件的花园面积能达到120m2吗?若能,求出此时BC的值;若不能,说明理由.
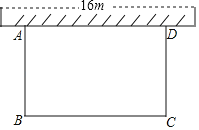
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合探究
已知抛物线y=ax2+![]() x+4的对称轴是直线x=3,与x轴相交于A,B两点(点B在点A右侧),与y轴交于点C.
x+4的对称轴是直线x=3,与x轴相交于A,B两点(点B在点A右侧),与y轴交于点C.
(1)求抛物线的解析式和A,B两点的坐标;
(2)如图1,若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),是否存在点P,使四边形PBOC的面积最大?若存在,求点P的坐标及四边形PBOC面积的最大值;若不存在,请说明理由;
(3)如图2,若点M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,直接写出点M的坐标.
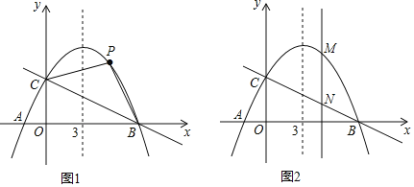
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com