
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
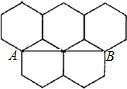 如图是由5个形状、大小完全相同的正六边形组成的图案,我们把正六边形的顶点称为格点.若Rt△ABC的顶点都在格点上,且AB为Rt△ABC的斜边,则Rt△ABC的个数有( )
如图是由5个形状、大小完全相同的正六边形组成的图案,我们把正六边形的顶点称为格点.若Rt△ABC的顶点都在格点上,且AB为Rt△ABC的斜边,则Rt△ABC的个数有( )| A. | 2个 | B. | 4个 | C. | 6个 | D. | 8个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小亮从家步行到公交站台,等公交去学校,图中的折线表示小亮的行程s(千米)与所花时间t(分钟)之间的函数关系.下列说法错误的是( )
小亮从家步行到公交站台,等公交去学校,图中的折线表示小亮的行程s(千米)与所花时间t(分钟)之间的函数关系.下列说法错误的是( )| A. | 小亮行程8千米,共用了30分钟 | B. | 小亮等公交车时间为6分钟 | ||
| C. | 小亮步行的速度是100米/分钟 | D. | 公交车的速度是350米/分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,小明想知道学校旗杆的高度,他把升旗绳子一端挂在旗杆顶端,发现绳子垂到地面时还余1m;当他把绳子下端拉开5m后,绳子下端刚好接触到地面,则旗杆高度为12m.
如图,小明想知道学校旗杆的高度,他把升旗绳子一端挂在旗杆顶端,发现绳子垂到地面时还余1m;当他把绳子下端拉开5m后,绳子下端刚好接触到地面,则旗杆高度为12m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
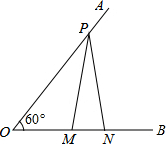 如图,已知∠AOB=60°,点P在边OA上,OP=20,点M,N在边OB上,PM=PN.若MN=6,则OM=( )
如图,已知∠AOB=60°,点P在边OA上,OP=20,点M,N在边OB上,PM=PN.若MN=6,则OM=( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com