
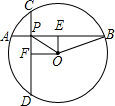
 如图,在⊙O中,弦AB=CD,AB⊥CD,垂足为P,OE⊥AB于E,OF⊥CD于F,
如图,在⊙O中,弦AB=CD,AB⊥CD,垂足为P,OE⊥AB于E,OF⊥CD于F,| 2 |
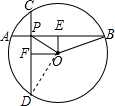 解:(1)四边形OFPE是正方形.
解:(1)四边形OFPE是正方形. | 1 |
| 2 |
| 1 |
| 2 |
|
|
|
| OB2-OE2 |
| 52-32 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
设∠BOC=α,∴∠BOD=3∠BOC=3α,∴∠COD=∠BOD-∠BOC=2α,∴∠AOD=
∴∠AOD=∠COD=2α,∴∠AOB=∠AOD+∠BOD=2α+3α=5α=70°,∴α=14°,∴∠BOC=14° |

查看答案和解析>>
科目:初中数学 来源: 题型:
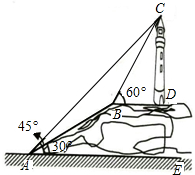 如图,某教学学习小组为了测量山顶上一古灯塔的高度CD,他们在山脚下的点A处测得塔顶C处的仰角为45°,沿着坡角为30°的登山梯AB向上走200米到达山顶B处后,测得塔顶C处的仰角为60°,已知点B与底部D在同一水平线上.
如图,某教学学习小组为了测量山顶上一古灯塔的高度CD,他们在山脚下的点A处测得塔顶C处的仰角为45°,沿着坡角为30°的登山梯AB向上走200米到达山顶B处后,测得塔顶C处的仰角为60°,已知点B与底部D在同一水平线上.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,下列结论中,正确的是( )
如图,下列结论中,正确的是( )| A、∠DAC与∠ACB是一对同位角 |
| B、若∠DAC=∠ACB,则AB∥CD |
| C、∠D与∠DAC是一对同旁内角 |
| D、若∠D=∠B,则AD∥BC |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com