
分析 根据有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘.任何数同零相乘,都得0.
解答 解:(1)(-2)×3×(+4)×(-1)
=-6×(+4)×(-1)
=-24×(-1)
=24;
(2)(-5)×(-5)×(-5)×2
=25×(-5)×2
=25×(-10)
=-250;
(3)(-$\frac{3}{7}$)×(-$\frac{4}{5}$)×(-$\frac{7}{12}$)
=$\frac{12}{35}$×(-$\frac{7}{12}$)
=-$\frac{1}{5}$;
(4)(-5)×(-$\frac{3}{32}$)×$\frac{7}{30}$×0×(-325)
=0.
点评 本题主要考查了有理数的乘法法则的运用,解题时注意:几个数相乘,有一个因数为0,积就为0.运用乘法法则,先确定符号,再把绝对值相乘. 多个因数相乘,看0因数和积的符号当先,这样做使运算既准确又简单.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,P是⊙O外动点,PA,PB,CD是⊙O的三条切线,C,D分别在PA,PB上,连接OC,OD,设∠P为x°,∠COD为y°,则y与x之间的函数关系式为y=90-$\frac{1}{2}$x.
如图,P是⊙O外动点,PA,PB,CD是⊙O的三条切线,C,D分别在PA,PB上,连接OC,OD,设∠P为x°,∠COD为y°,则y与x之间的函数关系式为y=90-$\frac{1}{2}$x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
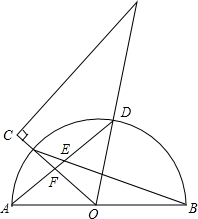 如图,半圆O中,将一块含60°的直角三角板的60°角顶点与圆心O重合,角的两条边分别与半圆圆弧交于C,D两点(点C在∠AOD内部),AD与BC交于点E,AD与OC交于点F.
如图,半圆O中,将一块含60°的直角三角板的60°角顶点与圆心O重合,角的两条边分别与半圆圆弧交于C,D两点(点C在∠AOD内部),AD与BC交于点E,AD与OC交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com