
【题目】计算(或化简)下列各题
(1)(+4.3)﹣(﹣4)+(﹣2.3)﹣(+4)
(2)﹣42÷(﹣2)3+|﹣![]() |×(﹣8)
|×(﹣8)
(3)(﹣36)×(![]() )
)
(4)(﹣3)2﹣[(﹣![]() )+(﹣
)+(﹣![]() )]÷
)]÷![]()
(5)2(m﹣1)﹣(2m﹣3)
(6)(5ab+3a2)﹣2(a2+2ab)
(7)先化简,再求值:![]() x﹣2(x﹣
x﹣2(x﹣![]() y)+(﹣
y)+(﹣![]() x+
x+![]() y),其中x=﹣2,y=
y),其中x=﹣2,y=![]() .
.
【答案】(1)2 (2)![]() (3)18 (4)20 (5)1 (6)
(3)18 (4)20 (5)1 (6)![]() (7)
(7)![]() ;
;![]()
【解析】
(1)原式利用减法法则变形,计算即可得到结果;
(2)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
(3)原式利用乘法分配律计算即可得到结果;
(4)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可得到结果;
(5)先去括号,再合并同类项即可得到结果;
(6)先去括号,再合并同类项即可得到结果;
(7)先去括号,再合并同类项,并将x的值代入即可得到结果;
(1)(+4.3)﹣(﹣4)+(﹣2.3)﹣(+4),
=4.3+4﹣2.3﹣4
=2;
(2)﹣42÷(﹣2)3+|﹣![]() |×(﹣8),
|×(﹣8),
=﹣16÷(﹣8)+![]() ×(﹣8)
×(﹣8)
=2﹣![]()
=![]() ;
;
(3)(﹣36)×(![]() ),
),
=﹣36×![]() +36×
+36×![]() +36×
+36×![]() ,
,
=﹣45+30+33,
=18;
(4)(﹣3)2﹣[(﹣![]() )+(﹣
)+(﹣![]() )]÷
)]÷![]() ,
,
=9﹣(﹣![]() )×12,
)×12,
=9﹣12×![]() +12×
+12×![]() ,
,
=9+8+3,
=20;
(5)2(m﹣1)﹣(2m﹣3)
=2m﹣2﹣2m+3
=1;
(6)(5ab+3a2)﹣2(a2+2ab)
=5ab+3a2﹣2a2﹣4ab
=ab+a2,
7)![]() x﹣2(x﹣
x﹣2(x﹣![]() y)+(﹣
y)+(﹣![]() x+
x+![]() y)
y)
=![]() x﹣2x+
x﹣2x+![]() y﹣
y﹣![]() x+
x+![]() y
y
=﹣3x+y,
当x=﹣2,y=![]() 时,原式=﹣3×(﹣2)+
时,原式=﹣3×(﹣2)+![]() =6
=6![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点
),点![]() 是
是![]() 轴正半轴上的一动点,以
轴正半轴上的一动点,以![]() 为边作等腰直角
为边作等腰直角![]() ,使
,使![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的纵坐标为
的纵坐标为![]() ,能表示
,能表示![]() 与
与![]() 的函数关系的图象大致是
的函数关系的图象大致是
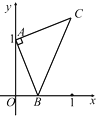
A. 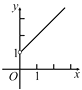 B.
B. 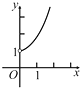 C.
C. 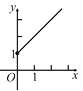 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() .求BE的长.
.求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题发现】
(1)如图(1),四边形ABCD中,若AB=AD,CB=CD,则线段BD,AC的位置关系为__________;
【拓展探究】
(2)如图(2),在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在Rt△ABC外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;
【解决问题】
(3)如图(3),在正方形ABCD中,AB=2![]() ,以点A为旋转中心将正方形ABCD旋转60°,得到正方形AB'C'D',请直接写出BD'平方的值.
,以点A为旋转中心将正方形ABCD旋转60°,得到正方形AB'C'D',请直接写出BD'平方的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个二次函数的图象经过A(0,﹣6)、B(4,﹣6)、C(6,0)三点.
(1)求这个二次函数的解析式;
(2)分别联结AC、BC,求tan∠ACB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市区自2014年1月起,居民生活用水开始实行阶梯式计量水价,该阶梯式计量水价分为三级(如下表所示):
月用水量(吨) | 水价(元/吨) |
第一级 20吨以下(含20吨) | 1.6 |
第二级 20吨﹣30吨(含30吨) | 2.4 |
第三级 30吨以上 | 3.2 |
例:某用户的月用水量为32吨,按三级计量应缴水费为:
1.6×20+2.4×10+3.2×2=62.4(元)
(1)如果甲用户的月用水量为12吨,则甲需缴的水费为 元;
(2)如果乙用户缴的水费为39.2元,则乙月用水量 吨;
(3)如果丙用户的月用水量为a吨,则丙用户该月应缴水费多少元?(用含a的代数式表示,并化简)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图22,将—矩形OABC放在直角坐际系中,O为坐标原点.点A在x轴正半轴上.点E是边AB上的—个动点(不与点A、N重合),过点E的反比例函数![]() 的图象与边BC交于点F。
的图象与边BC交于点F。
【1】若△OAE、△OCF的而积分别为S1、S2.且S1+S2=2,求![]() 的值:
的值:
【2】若OA=2.0C=4.问当点E运动到什么位置时,四边形OAEF的面积最大.其最大值为多少?
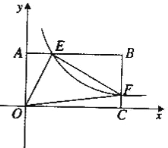
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在边BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画出图表示.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com