
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.

(1)求该抛物线的解析式;
(2)用配方法求该抛物线的对称轴以及顶点坐标;
(3)根据图象回答,当x为何值时,y>0,当x为何值时,y<0.
【答案】(1)抛物线的解析式为:y=x2﹣2x﹣3;
(2)y=(x﹣1)2﹣4,该抛物线的对称轴为直线x=1,顶点坐标为:(1,﹣4);
(3)当x<﹣1或x>3时,y>0,当﹣1<x<3时,y<0.
【解析】
试题分析:(1)直接利用待定系数法求二次函数解析式得出答案;
(2)直接利用配方法求出二次函数对称轴和顶点坐标即可;
(3)利用A,B点坐标,再结合函数图象得出x的取值范围.
解:(1)将A(﹣1,0),B(3,0)两点代入y=x2+bx+c得:
![]() ,
,
解得:![]() ,
,
故抛物线的解析式为:y=x2﹣2x﹣3;
(2)y=x2﹣2x﹣3
=(x﹣1)2﹣4,
故该抛物线的对称轴为直线x=1,顶点坐标为:(1,﹣4);
(3)如图所示:当x<﹣1或x>3时,y>0,当﹣1<x<3时,y<0.


科目:初中数学 来源: 题型:
【题目】某商店在甲批发市场以每包m元的价格进了40包茶叶,又在乙批发市场以每包n元(m>n)的价格进了同样的60包茶叶,如果商家以每包![]() 元的价格卖出这种茶叶,卖完后,这家商店( )
元的价格卖出这种茶叶,卖完后,这家商店( )
A.盈利了
B.亏损了
C.不赢不亏
D.盈亏不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
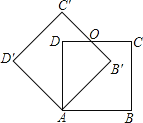
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转45度后得到正方形AB′C′D′,边B′C′与DC交于点O,则四边形AB′OD的周长是( )
A.2 ![]() B.3 C.
B.3 C.![]() D.1+
D.1+![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com