
【题目】对于某一函数给出如下定义:对于任意实数m, 当自变量x≥m时,函数y关于x的函数图象为![]() ,将G沿直线x=m翻折后得到的函数图象为
,将G沿直线x=m翻折后得到的函数图象为![]() ,函数G的图象由
,函数G的图象由![]() 和
和![]() 两部分共同组成,则函数G为原函数的“对折函数”,如函数y=x(x≥2)的对折函数为
两部分共同组成,则函数G为原函数的“对折函数”,如函数y=x(x≥2)的对折函数为![]()
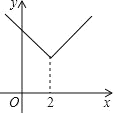
(1)写出函数y =2x+1(x≥ 1)的对折函数;
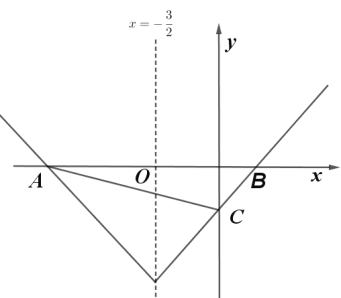
(2)若函数y =2x2(x≥![]() )的对折函数与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,求△ABC的周长;
)的对折函数与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,求△ABC的周长;
(3)若点P(m,5)在函数y =![]() 4( x≥1)的对折函数的图象上,求m的值;
4( x≥1)的对折函数的图象上,求m的值;
(4)当函数y=![]() 4(x≥n)的对折函数与x轴有不同的交点个数时,直接写出n的取值范围
4(x≥n)的对折函数与x轴有不同的交点个数时,直接写出n的取值范围
【答案】(1)![]() ;(2)
;(2)![]() ;(3)m=4或6;(4)①当n<1时,有4个交点;②当n=1时,有3个交点;③当1<n<3时,函数与x轴有2个交点;④当n=3时,有3个交点;⑤当n>3时,无交点
;(3)m=4或6;(4)①当n<1时,有4个交点;②当n=1时,有3个交点;③当1<n<3时,函数与x轴有2个交点;④当n=3时,有3个交点;⑤当n>3时,无交点
【解析】
(1)利用对折函数的定义求解对折后的函数与![]() 轴的交点坐标,利用待定系数法求解即可;
轴的交点坐标,利用待定系数法求解即可;
(2)先求解对折函数的解析式,得到C的坐标,利用勾股定理可得答案;
(3)先求解对折函数的解析式,把P的坐标代入即可得到答案;
(4)根据拐点的纵坐标分情况讨论,即可得到对折函数的图像,根据图像可得答案.
(1)如图1,设对折点为A,则点A(1,3),设对折图象与x轴的交点为A. B,
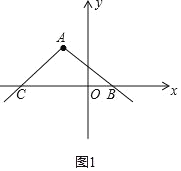
当y =2x+1=0时,x=![]() 时,即点B(
时,即点B(![]() ,0),则点C(
,0),则点C(![]() ,0),
,0),
设直线AC为:![]()
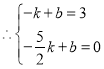
解得:![]()
所以:直线AC的表达式为:y=2x+5,
故y=2x+1(x1)的对折函数为:![]()
(2)由对折函数的定义得拐点坐标为:![]() ,
,![]() ,
,
![]()
同理可得:函数y=2x2(![]() )的对折函数
)的对折函数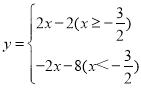
![]() 点C(0,2),
点C(0,2),
则AB=5,AC=![]() ,BC=
,BC=![]() ,
,
则△ABC的周长为:![]()
(3)令y=![]() 4=0,则x=1或3,如下图:即点A. B的坐标为(1,0)、(3,0),
4=0,则x=1或3,如下图:即点A. B的坐标为(1,0)、(3,0),
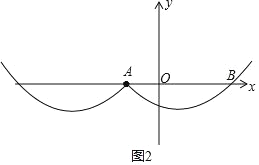
则对折后函数的顶点坐标为(3,4),该函数表达式为:y=![]() 4,
4,
即对折函数为![]()
将点P(m,5)代入y=![]() 4得:
4得:
![]()
解得:![]() (舍去)
(舍去)
将点P(m,5)代入y=![]() 4,
4,
![]()
解得:![]() (舍去)
(舍去)
综上:m=4或6
(4)①当n<1时,如图3:
此时x=n在点A(1,0)的左侧,
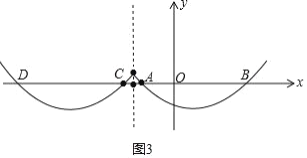
从图中可以看出:函数与x轴有4个交点(A、B. C. D);
②当n=1时,x=n过点A,从图2可以看出:函数与x轴有3个交点;
③如图:同理:当1<n<3时,函数与x轴有2个交点;
④如图:同理:当n=3时,函数与x轴有3个交点;
⑤同理:当n>3时,无交点


科目:初中数学 来源: 题型:
【题目】五张正面分别写有数字:﹣3,﹣2,0,1,2的卡片,它们的背面完全相同,现将这五张卡片背面朝上洗匀.
(1)从中任意抽取一张卡片,则所抽卡片上数字的绝对值不小于1的概率是 ;
(2)先从中任意抽取一张卡片,以其正面数字作为m的值,然后再从剩余的卡片中随机抽一张,以其正面的数字作为n的值,请用列表法或画树状图法,求点Q(m,n)在第四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,![]() ,顶点C的坐标为
,顶点C的坐标为![]() ,x反比例函数
,x反比例函数![]() 的图象与菱形对角线AO交于点D,连接BD,当
的图象与菱形对角线AO交于点D,连接BD,当![]() 轴时,k的值是______.
轴时,k的值是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三年级教师对试卷讲评课中学生参与的深度和广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题:
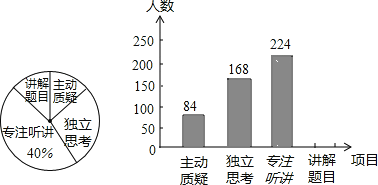
(1)在这次评价中,一共抽查了 名学生;
(2)请将条形统计图补充完整;
(3)如果全市有12000名初中学生,那么在试卷讲评课中,独立思考的学生约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用A、B两种机器人搬运大米,A型机器人比B型机器人每小时多搬运20袋大米,A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等.求A、B型机器人每小时分别搬运多少袋大米.
查看答案和解析>>
科目:初中数学 来源: 题型:
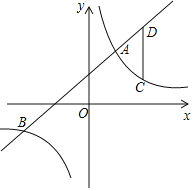
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象相交于A(2,4),B(n,﹣2)两点.
(m≠0)的图象相交于A(2,4),B(n,﹣2)两点.
(1)求一次函数和反比例函数的表达式;
(2)点C是第一象限内反比例函数图象上的一点,且点C在A的右侧,过点C作CD平行于y轴交直线AB于点D,若以C为圆心,CD长为半径的⊙C恰好与y轴相切,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
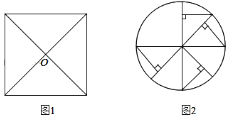
【题目】规定:在平面内,如果一个图形绕一个定点旋转一定的角度α(0°<α≤180°)后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角度α称为这个图形的一个旋转角.例如:正方形绕着两条对角线的交点O旋转90°或180°后,能与自身重合(如图1),所以正方形是旋转对称图形,且有两个旋转角.根据以上规定,回答问题:
(1)下列图形是旋转对称图形,但不是中心对称图形的是________;
A.矩形 B.正五边形 C.菱形 D.正六边形
(2)下列图形中,是旋转对称图形,且有一个旋转角是60度的有:________(填序号);

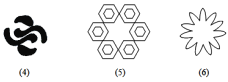
(3)下列三个命题:①中心对称图形是旋转对称图形;②等腰三角形是旋转对称图形;③圆是旋转对称图形,其中真命题的个数有( )个;
A.0 B.1 C.2 D.3
(4)如图2的旋转对称图形由等腰直角三角形和圆构成,旋转角有45°,90°,135°,180°,将图形补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快餐店外卖促销,佳佳和点点想点外卖,每单需支付送餐费5元,每种餐食外卖价格如下表:
餐食种类 | 价格(单位:元) |
汉堡套餐 | 40 |
鸡翅 | 16 |
鸡块 | 15 |
冰激凌 | 14 |
蔬菜沙拉 | 9 |
促销活动:
(1)汉堡套餐5折优惠,每单仅限一套;
(2)全部商品(包括打折套餐)满20元减4元,满40元减10元,满60元减15元,满80元减20元.
佳佳想要汉堡套餐、鸡翅、冰激凌、蔬菜沙拉各一份;点点想要汉堡套餐、鸡块、冰激凌各一份,若他们把想要的都买全,最少要花____________元(含送餐费).
查看答案和解析>>
科目:初中数学 来源: 题型:
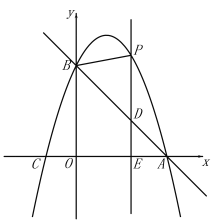
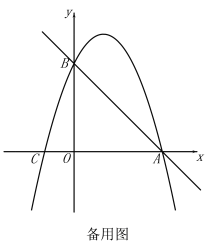
【题目】如图,直线![]() 与x轴交于点A(3,0),与y轴交于点B,抛物线
与x轴交于点A(3,0),与y轴交于点B,抛物线![]() 经过A,B.
经过A,B.
(1)求抛物线解析式;
(2)E(m,0)是x轴上一动点,过点E作![]() 轴于点E,交直线AB于点D,交抛物线于点P,连接PB.
轴于点E,交直线AB于点D,交抛物线于点P,连接PB.
①点E在线段OA上运动,若△PBD是等腰三角形时,求点E的坐标;
②点E在x轴的正半轴上运动,若![]() ,请直接写出m的值.
,请直接写出m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com