
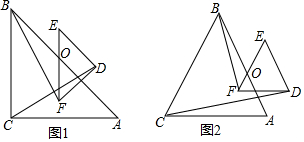
分析 (1)如图1中,猜想:BF=CD,BF⊥CD.只要证明△BOF≌△COD即可解决问题;
(2)如图2中,结论:$\frac{BF}{CD}$=$\frac{\sqrt{3}}{3}$.BF⊥CD,只要证明△BOF∽△COD,相似比为 $\frac{\sqrt{3}}{3}$即可解决问题;
(3)如图3中连接OC、OD,只要证明△BOF∽△COD,相似比为tan $\frac{α}{2}$即可解决问题;
解答 解:(1)猜想:BF=CD,BF⊥CD.理由如下:
如图1中所示,连接OC、OD,延长BF交CD于H,OC交BF于K.
∵△ABC为等腰直角三角形,点O为斜边AB的中点,
∴OB=OC,∠BOC=90°.
∵△DEF为等腰直角三角形,点O为斜边EF的中点,
∴OF=OD,∠DOF=90°.
∵∠BOF=∠BOC+∠COF=90°+∠COF,∠COD=∠DOF+∠COF=90°+∠COF,
∴∠BOF=∠COD.
∵在△BOF与△COD中,
$\left\{\begin{array}{l}{OB=OC}\\{∠BOF=∠COD}\\{OF=OD}\end{array}\right.$,
∴△BOF≌△COD(SAS),
∴BF=CD,∴∠OBF=∠OCD,
∵∠OBF+∠BKO=90°,∠BKO=∠CKH,
∴∠OCD+∠CKH=90°,
∴∠BHC=90°,
∴BF⊥CD,BF=CD.
(2)结论:$\frac{BF}{CD}$=$\frac{\sqrt{3}}{3}$.BF⊥CD,
如答2中,连接OC、OD,延长BF交CD于H,OC交BF于K
∵△ABC为等边三角形,点O为边AB的中点,
∴$\frac{OB}{OC}$=tan30°=$\frac{\sqrt{3}}{3}$,∠BOC=90°.
∵△DEF为等边三角形,点O为边EF的中点,
∴$\frac{OF}{OD}$=tan30°=$\frac{\sqrt{3}}{3}$,∠DOF=90°.
∴$\frac{OB}{OC}$=$\frac{OF}{OD}$=$\frac{\sqrt{3}}{3}$.
∵∠BOF=∠BOC+∠COF=90°+∠COF,∠COD=∠DOF+∠COF=90°+∠COF,
∴∠BOF=∠COD.
在△BOF与△COD中,
∵$\frac{OB}{OC}$=$\frac{OF}{OD}$=$\frac{\sqrt{3}}{3}$,∠BOF=∠COD,
∴△BOF∽△COD,
∴$\frac{BF}{CD}$=$\frac{\sqrt{3}}{3}$,∠OBF=∠OCD,
∵∠OBF+∠BKO=90°,∠BKO=∠CKH,
∴∠OCD+∠CKH=90°,
∴∠BHC=90°,
∴BF⊥CD,$\frac{BF}{CD}$=$\frac{\sqrt{3}}{3}$.
(3)如答图④所示,连接OC、OD.
∵△ABC为等腰三角形,点O为底边AB的中点,
∴$\frac{OB}{OC}$=tan $\frac{α}{2}$,∠BOC=90°.
∵△DEF为等腰三角形,点O为底边EF的中点,
∴$\frac{OF}{OD}$=tan $\frac{α}{2}$,∠DOF=90°.
∴$\frac{OB}{OC}$=$\frac{OF}{OD}$=tan $\frac{α}{2}$.
∵∠BOF=∠BOC+∠COF=90°+∠COF,∠COD=∠DOF+∠COF=90°+∠COF,
∴∠BOF=∠COD.
在△BOF与△COD中,
∵$\frac{OB}{OC}$=$\frac{OF}{OD}$=tan $\frac{α}{2}$,∠BOF=∠COD,
∴△BOF∽△COD,
∴$\frac{BF}{CD}$=tan $\frac{α}{2}$.
点评 本题考查相似三角形综合题、全等三角形的判定与性质.解题关键是:第一,善于发现几何变换中不变的逻辑关系,即△BOF≌△COD或△BOF∽△COD;第二,熟练运用等腰直角三角形、等边三角形、等腰三角形的相关性质.本题(1)(2)(3)问的解题思路一脉相承,由特殊到一般,有利于同学们进行学习与探究.


科目:初中数学 来源: 题型:解答题
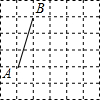 如图,在所给的6×6网格中每个小正方形的边长都为1,线段AB的端点都在格点上,按下列要求画正方形(另两个顶点也都在格点上),并直接写出所画正方形的面积.
如图,在所给的6×6网格中每个小正方形的边长都为1,线段AB的端点都在格点上,按下列要求画正方形(另两个顶点也都在格点上),并直接写出所画正方形的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
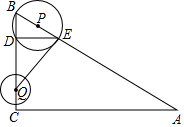 如图,在△ABC中,∠ACB为直角,AB=10,∠A=30°,半径为1的动圆Q的圆心从点C出发,沿着CB方向以1个单位长度/秒的速度匀速运动,同时动点P从点B出发,沿着BA方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PB长为半径的⊙P与AB、BC的另一个交点分别为E、D,连结ED、EQ.
如图,在△ABC中,∠ACB为直角,AB=10,∠A=30°,半径为1的动圆Q的圆心从点C出发,沿着CB方向以1个单位长度/秒的速度匀速运动,同时动点P从点B出发,沿着BA方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PB长为半径的⊙P与AB、BC的另一个交点分别为E、D,连结ED、EQ.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线DE与直线AB、CD分别交于点E、D、EG平分∠DEB,直线GF与直线AB交于点F,若∠CDE=116°,∠AFG=130°,∠G=8°.判断直线AB、CD是否平行?并说明理由.
如图,直线DE与直线AB、CD分别交于点E、D、EG平分∠DEB,直线GF与直线AB交于点F,若∠CDE=116°,∠AFG=130°,∠G=8°.判断直线AB、CD是否平行?并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若|m|=|n|,则m=n | B. | 若a2>b2,则a>b | C. | 若$\root{3}{a}=\root{3}{b}$,则a=b | D. | 若$\sqrt{a^2}={(\sqrt{b})^2}$,则a=b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
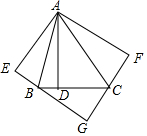 如图,在△ABC中,∠BAC=45°,AD⊥BC于点D,$\frac{BD}{DC}$=$\frac{2}{3}$,AD=6,将△ADB,△ADC分别沿AB,AC翻折得△ABE,△ACF,延长EB,FC相交于点G.
如图,在△ABC中,∠BAC=45°,AD⊥BC于点D,$\frac{BD}{DC}$=$\frac{2}{3}$,AD=6,将△ADB,△ADC分别沿AB,AC翻折得△ABE,△ACF,延长EB,FC相交于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com