
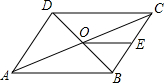
 如图,在?ABCD中,对角线AC,BD交于点O,OE∥DC交BC于点E,若△BEO的面积为1,则?ABCD的面积等于8.
如图,在?ABCD中,对角线AC,BD交于点O,OE∥DC交BC于点E,若△BEO的面积为1,则?ABCD的面积等于8.  培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
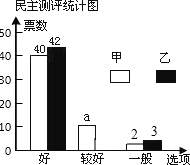 九年级一班邀请A、B、C、D、E五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投费,绘制了如下的统计表和不完整的条形统计图:
九年级一班邀请A、B、C、D、E五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投费,绘制了如下的统计表和不完整的条形统计图:| A | B | C | D | E | |
| 甲 | 89 | 91 | 93 | 94 | 86 |
| 乙 | 88 | 87 | 90 | 98 | 92 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
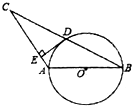 如图,⊙O的直径AB=4,sin∠ABC=$\frac{1}{2}$,BC交⊙O于D,D是BC的中点.
如图,⊙O的直径AB=4,sin∠ABC=$\frac{1}{2}$,BC交⊙O于D,D是BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.620×1011 | B. | 6.20×1010 | C. | 6.20×109 | D. | 6.20×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形OABC的边OA在x轴上,双曲线y=$\frac{k}{x}$与BC交于点D,与AB交于点E,DE=$\frac{1}{2}$OB,矩形OABC的面积为4,则k的值为2.
如图,矩形OABC的边OA在x轴上,双曲线y=$\frac{k}{x}$与BC交于点D,与AB交于点E,DE=$\frac{1}{2}$OB,矩形OABC的面积为4,则k的值为2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com