
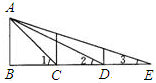
 如图,∠B=90°,AB=BC=CD=DE,那么下列结论正确是( )
如图,∠B=90°,AB=BC=CD=DE,那么下列结论正确是( )| A. | ∠1+∠2+∠3=135° | B. | △ABD∽△EBA | C. | △ACD∽△ECA | D. | 以上结论都不对 |
分析 根据AB=AC,∠B=90°,可以求得∠1=45°,设AB=BC=CD=DE=1,即可求证△ACD∽△ECA.
解答 解:∵AB=BC,∠B=90°,
∴∠1=45°.
设AB=BC=CD=DE=1,则AC=$\sqrt{2}$,CE=2,
∴$\frac{CD}{AC}$=$\frac{1}{\sqrt{2}}$,$\frac{AC}{CE}$=$\frac{\sqrt{2}}{2}$=$\frac{1}{\sqrt{2}}$,
∵∠ACD=∠ACE,
∴△ACE∽△DCA,
故选C.
点评 本题考查了相似三角形的性质/等腰直角三角形的性质、勾股定理等知识,解题的关键是正确寻找相似三角形,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | x<-1 | B. | x≥3 | C. | -1<x≤3 | D. | 无解 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
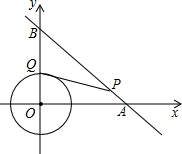 如图,⊙O是以原点为圆心,2$\sqrt{3}$为半径的圆,点P是直线上y=-x+8的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
如图,⊙O是以原点为圆心,2$\sqrt{3}$为半径的圆,点P是直线上y=-x+8的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )| A. | 4 | B. | 2$\sqrt{5}$ | C. | 8-2$\sqrt{3}$ | D. | 2$\sqrt{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x+y=3 | B. | x+y=-3 | C. | x+y=-9 | D. | x+y=9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
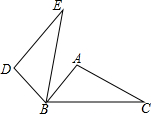 如图,△ABC中,∠ABC=50°,∠C=30°,将△ABC绕点B逆时针旋转α(0°<α≤90°)得到△DBE,若DE∥AB,则α为( )
如图,△ABC中,∠ABC=50°,∠C=30°,将△ABC绕点B逆时针旋转α(0°<α≤90°)得到△DBE,若DE∥AB,则α为( )| A. | 50° | B. | 70° | C. | 80° | D. | 90° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△OAB中,OA=OB,∠AOB=15°,在△OCD中,OC=OD,∠COD=45°,且点C在边OA上,连接CB,将线段OB绕点O逆时针旋转一定角度得到线段OE,使得DE=CB,则∠BOE的度数为( )
如图,在△OAB中,OA=OB,∠AOB=15°,在△OCD中,OC=OD,∠COD=45°,且点C在边OA上,连接CB,将线段OB绕点O逆时针旋转一定角度得到线段OE,使得DE=CB,则∠BOE的度数为( )| A. | 15° | B. | 15°或45° | C. | 45° | D. | 45°或60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com