
分析 (1)首先连接OA,设这座拱桥所在圆的半径为x米,由垂径定理,易得方程:x2=(x-3)2+($\sqrt{21}$)2,解此方程即可求得答案;
(2)连接OM,设MN=4米,可求得此时OH的高,即可求得OH-OD-0.5的长,比较2米,即可得到此时船能否顺利通过这座弓行石桥.
解答 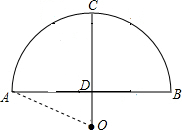 解:(1)连接OA,
解:(1)连接OA,
根据题意得:CD=3米,AB=2$\sqrt{21}$米,
则AD=$\frac{1}{2}$AB=$\sqrt{21}$(米),
设这座弓行石桥所在圆的半径为x米,
则OA=OC=x米,OD=OC-CD=(x-3)米,
在Rt△AOD中,OA2=OD2+AD2,
则x2=(x-3)2+($\sqrt{21}$)2,
解得:x=5,
故这座弓行石桥所在圆的半径为5米.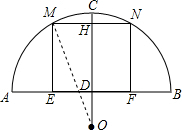 (2)货船能顺利通过这座弓行石桥.理由:
(2)货船能顺利通过这座弓行石桥.理由:
连接OM,
设MN=4米,
∵OC⊥MN,
∴MH=$\frac{1}{2}$MN=2(米),
在Rt△OMH中,OH=$\sqrt{O{M}^{2}-M{H}^{2}}$=$\sqrt{21}$(米),
∵OD=OC-CD=5-3=2(米)
∵OH-OD-0.5=$\sqrt{21}$-2.5>2,
∴此船能顺利通过这座弓行石桥.
点评 此题考查了垂径定理的应用.此题难度适中,关键在于利用弧形所在的圆,构造出直角三角形,根据勾股定理进行求解计算.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1,-8) | B. | (1,-2) | C. | (-6,-1) | D. | (0,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com