
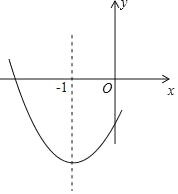
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的对称轴为直线x=﹣1,下列结论正确的有_____(填序号).
①若图象过点(﹣3,y1)、(2,y2),则y1<y2;
②ac<0;
③2a﹣b=0;
④b2﹣4ac<0.
【答案】①②③
【解析】
①根据抛物线的对称轴找到(﹣3,y1)的对称点(1,y1),再与(2,y2)根据函数的增减性进行比较;②由抛物线的开口方向及与y轴的交点位置,即可得出a>0、c<0,进而可得出ac<0,结论②正确;③由-![]() =-1可得出2a-b=0,结论③正确;④由抛物线与x轴有两个交点,结合根的判别式可得出△=b2-4ac>0,结论④错误.综上即可得出结论.
=-1可得出2a-b=0,结论③正确;④由抛物线与x轴有两个交点,结合根的判别式可得出△=b2-4ac>0,结论④错误.综上即可得出结论.
解:①∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,
∴(﹣3,y1)的对称点是(1,y1),
∵抛物线的开口向上,
∴对称轴右侧y随x的增大而增大,
∴1<2,则y1<y2,
故①正确;
②∵抛物线的开口向上,
∴a>0,
∵抛物线与y轴交于y轴的负半轴,
∴c<0,
∴ac<0,
故②正确;
③∵抛物线的对称轴是x=-1,
∴-![]() =-1,
=-1,
∴b=2a,
∴2a-b=0,
故③正确;
④∵抛物线与x轴有两个交点,
∴△=b2-4ac>0,
故④错误.
故答案为:①②③.


科目:初中数学 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课中,同学们准备了一些等腰直角三角形纸片,从每张纸片中剪出一个扇形制作圆锥玩具模型.如图,已知△ABC是腰长为16cm的等腰直角三角形.
(1)在等腰直角三角形ABC纸片中,以C为圆心,剪出一个面积最大的扇形(要求:尺规作图,保留作图痕迹,不写作法);
(2)请求出所制作圆锥底面的半径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.
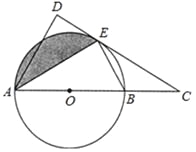
(1)求证:AE平分∠DAC;
(2)若AB=4,∠ABE=60°.
①求AD的长;
②求出图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
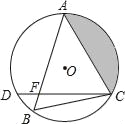
【题目】如图所示,在⊙O中,![]() ,弦CD与弦AB交于点F,连接BC,若∠ACD=60°,⊙O的半径长为2cm.
,弦CD与弦AB交于点F,连接BC,若∠ACD=60°,⊙O的半径长为2cm.
(1)求∠B的度数及圆心O到弦AC的距离;
(2)求图中阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量某建筑物EF的高度,小明在楼AB上选择观测点A、C,从A测得建筑物的顶部E的仰角为37°,从C测得建筑物的顶部E的仰角为45°,A处高度为20m,C处高度为10m.求建筑物EF的高度(精确到1m).
(参考数据:sin37°≈0.6,cos37°≈0.8,tan37≈0.75,![]() ≈1.4)
≈1.4)

查看答案和解析>>
科目:初中数学 来源: 题型:
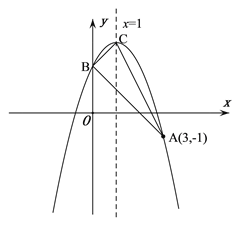
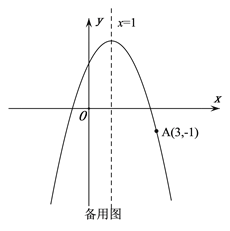
【题目】如图,抛物线![]() 的顶点为C,对称轴为直线
的顶点为C,对称轴为直线![]() ,且经过点A(3,-1),与y轴交于点B.
,且经过点A(3,-1),与y轴交于点B.
(1)求抛物线的解析式;
(2)判断△ABC的形状,并说明理由;
(3)经过点A的直线交抛物线于点P,交x轴于点Q,若![]() ,试求出点P的坐标.
,试求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
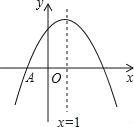
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②﹣1≤a≤﹣![]() ;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
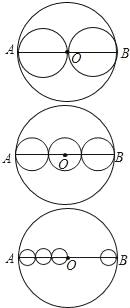
【题目】如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长l=πa.
计算:(1)把AB分成两条相等的线段,每个小圆的周长![]() ;
;
(2)把AB分成三条相等的线段,每个小圆的周长l3= ;
(3)把AB分成四条相等的线段,每个小圆的周长l4= ;
(4)把AB分成n条相等的线段,每个小圆的周长ln= .
结论:把大圆的直径分成n条相等的线段,以每条线段为直径分别画小圆,那么每个小圆周长是大圆周长的 .请仿照上面的探索方法和步骤,计算推导出每个小圆面积与大圆面积的关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com