
分析 (1)利用多项式乘以多项式法则计算得到结果,归纳总结得到一般性规律,即可确定出结果;
(2)利用得出的结果将原式变形,计算即可得到结果.
解答 解:(1)a2-1;a3-1;a4-1;a100-1;
故答案为:a2-1;a3-1;a4-1;a100-1;
(2)①(2-1)(299+298+297+…+22+2+1)=2100-1,由于2-1=1,
则299+298+297+…+22+2+1=2100-1;
②∵a6-1=(a-1)(a5+a4+a3+a2+a+1)=0,
∴a6=1,
∴a=±1,
但当a=1时,a5+a4+a3+a2+a+1=0不成立,
则a=-1.
点评 此题考查了平方差公式,以及规律型:数字的变化类,弄清题中的规律是解本题的关键.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
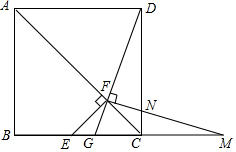 如图.在正方形ABCD中,点E是BC边上的中点,EF⊥AC于点F.连接DF并延长交BC于G.过F作FM⊥DG交CD于N,交BC的延长线于点M.
如图.在正方形ABCD中,点E是BC边上的中点,EF⊥AC于点F.连接DF并延长交BC于G.过F作FM⊥DG交CD于N,交BC的延长线于点M.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com