
【题目】近日,在公安部交通管理局部署下,全国各地交警都在大力开展|一盔一带安全守护行动,为了解市民对骑电动车戴头盔的赞同情况,某课题小组随机调查了部分市民,并根据调查结果绘制了尚不完整的统计图.
根据以上统计图回答一下问题:
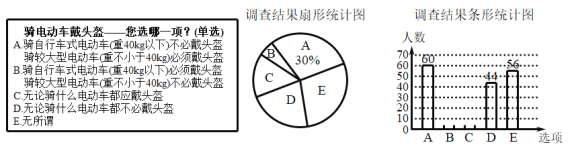
(1)这次调查的市民共_______人;
(2)若选择![]() 的人数是选择
的人数是选择![]() 的人数的3倍,则扇形统计图中,扇形
的人数的3倍,则扇形统计图中,扇形![]() 的圆心角度数是______;
的圆心角度数是______;
(3)补全条形统计图;
(4)若该市约有80万人,请估计安全意识淡薄(选择D或E)的人数.
【答案】(1)200;(2)100.8度;(3)补充完整条形图见解析;(4)该市有40万人.
【解析】
(1)用A的频数除以A所占的百分比即可;
(2)用(1)计算的总人数减去A、D、E求出B和C的人数和,然后设选择B的人数为x,则选择C的人数为3x,最后列方程求解即可求出B、C的频数;先求出E占调查人数的百分比,然后再乘360°即可;
(3)根据(2)的计算结果补全条形统计图即可;
(4)先求出D、E占调查人数的百分比,然后再乘以80万即可.
解:(1)60÷30%=200人;
(2)B和C的总人数为:200-60-44-56=40人
设选择B的人数为x,则选择C的人数为3x
则有:x+3x=40
解得x=10,3x=30
所以选择B、C的人数分别为10和30;
扇形![]() 的圆心角度数为:
的圆心角度数为:![]() =100.8°;
=100.8°;
(3)补全统计图如下:

(4)![]() 万人
万人
答:该市有40万人安全意识淡薄.


科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径,点
的直径,点![]() 是
是![]() 右侧半圆上的一个动点,点
右侧半圆上的一个动点,点![]() 是
是![]() 左侧半圆的中点,
左侧半圆的中点,![]() 是
是![]() 的切线,切点为
的切线,切点为![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .点
.点![]() 为射线
为射线![]() 上一动点,连接
上一动点,连接![]() ,
,![]()
![]() ,
,![]() .
.
(1)当![]() 时, 求证:
时, 求证:![]() .
.
(2)若![]() 的半径为
的半径为![]() ,请填空:
,请填空:
①当四边形![]() 为正方形时,
为正方形时,![]()
②当![]() 时, 四边形
时, 四边形![]() 为菱形.
为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
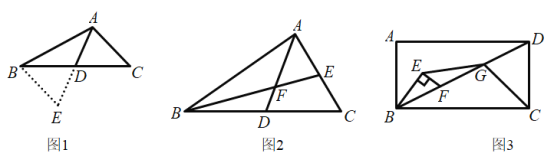
小红遇到这样一个问题:如图1,![]() 中,
中,![]() ,
,![]() ,AD是中线,求AD的取值范围.她的做法是:延长AD到E,使
,AD是中线,求AD的取值范围.她的做法是:延长AD到E,使![]() ,连接BE,证明
,连接BE,证明![]() ,经过推理和计算使问题得到解决.
,经过推理和计算使问题得到解决.
请回答:(1)小红证明![]() 的判定定理是:__________________________________________;
的判定定理是:__________________________________________;
(2)AD的取值范围是________________________;
方法运用:
(3)如图2,AD是![]() 的中线,在AD上取一点F,连结BF并延长交AC于点E,使
的中线,在AD上取一点F,连结BF并延长交AC于点E,使![]() ,求证:
,求证:![]() .
.
(4)如图3,在矩形ABCD中,![]() ,在BD上取一点F,以BF为斜边作
,在BD上取一点F,以BF为斜边作![]() ,且
,且![]() ,点G是DF的中点,连接EG,CG,求证:
,点G是DF的中点,连接EG,CG,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生每天的睡眠情况,某初中学校从全校800名学生中随机抽取了40名学生,调查了他们平均每天的睡眠时间(单位:h),统计结果如下:9,8,10.5,7,9,8,10,9.5,8,9,9.5,7.5,9.5,9,8.5,7.5,10,9.5,8,9,7,9.5,8.5,9,7,9,9,7.5,8.5,8.5,9,8,7.5,9.5,10,9.5,8.5,9,8,9.在对这些数据整理后,绘制了如图的统计图表:
睡眠时间分组统计表:
组别 | 睡眠时间分组 | 人数(频数) |
1 | 7≤t<8 | m |
2 | 8≤t<9 | 11 |
3 | 9≤t<10 | n |
4 | 10≤t<11 | 4 |
请根据以上信息,解答下列问题:
(1)m= ,n= ,a= ,b= ;
(2)抽取的这40名学生平均每天睡眠时间的中位数落在 组(填组别);在扇形统计图中,第4组所在扇形的圆心角是 度;
(3)如果按照学校要求,学生平均每天的睡眠时间应不少于9h.请估计该校学生中睡眠时间符合要求的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】筒车是我国古代利用水力驱动的灌溉工具,唐代陈廷章在《水轮赋》中写道:“水能利物,轮乃曲成”.如图,半径为![]() 的筒车
的筒车![]() 按逆时针方向每分钟转
按逆时针方向每分钟转![]() 圈,筒车与水面分别交于点
圈,筒车与水面分别交于点![]() 、
、![]() ,筒车的轴心
,筒车的轴心![]() 距离水面的高度
距离水面的高度![]() 长为
长为![]() ,简车上均匀分布着若干个盛水筒.若以某个盛水筒
,简车上均匀分布着若干个盛水筒.若以某个盛水筒![]() 刚浮出水面时开始计算时间.
刚浮出水面时开始计算时间.

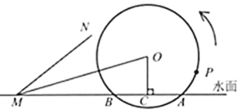
(1)经过多长时间,盛水筒![]() 首次到达最高点?
首次到达最高点?
(2)浮出水面3.4秒后,盛水筒![]() 距离水面多高?
距离水面多高?
(3)若接水槽![]() 所在直线是
所在直线是![]() 的切线,且与直线
的切线,且与直线![]() 交于点
交于点![]() ,
,![]() .求盛水筒
.求盛水筒![]() 从最高点开始,至少经过多长时间恰好在直线
从最高点开始,至少经过多长时间恰好在直线![]() 上.(参考数据:
上.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在菱形ABCD中,![]() ,点E,F分别是AC,AB上的点,且
,点E,F分别是AC,AB上的点,且![]() ,猜想:
,猜想:
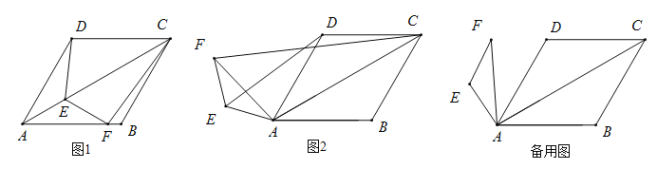
①![]() 的值是_______;
的值是_______;
②直线DE与直线CF所成的角中较小的角的度数是_______.
(2)类比探究:如图2,将绕![]() 点A逆时针旋转,在旋转的过程中,(1)中结论是否成立,就图2的情形说明理由.
点A逆时针旋转,在旋转的过程中,(1)中结论是否成立,就图2的情形说明理由.
(3)拓展延伸:
在![]() 绕点A旋转的过程中,当
绕点A旋转的过程中,当![]() 三点共线时,请直接写出CF的长.
三点共线时,请直接写出CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”;数形结合是解决数学问题的重要思想方法.例如,代数式![]() 的几何意义是数轴上
的几何意义是数轴上![]() 所对应的点与2所对应的点之间的距离;因为
所对应的点与2所对应的点之间的距离;因为![]() ,所以
,所以![]() 的几何意义就是数轴上
的几何意义就是数轴上![]() 所对应的点与
所对应的点与![]() 所对应的点之间的距离.
所对应的点之间的距离.
⑴. 发现问题:代数式![]() 的最小值是多少?
的最小值是多少?
⑵. 探究问题:如图,点![]() 分别表示的是
分别表示的是![]() ,
,![]() .
.
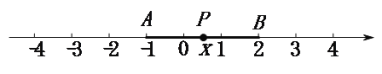
∵![]() 的几何意义是线段
的几何意义是线段![]() 与
与![]() 的长度之和
的长度之和
∴当点![]() 在线段
在线段![]() 上时,
上时,![]() ;当点点
;当点点![]() 在点
在点![]() 的左侧或点
的左侧或点![]() 的右侧时
的右侧时 ![]()
∴![]() 的最小值是3.
的最小值是3.
⑶.解决问题:
①.![]() 的最小值是 ;
的最小值是 ;
②.利用上述思想方法解不等式:![]()
![]()
③.当![]() 为何值时,代数式
为何值时,代数式![]() 的最小值是2.
的最小值是2.
查看答案和解析>>
科目:初中数学 来源: 题型:
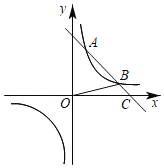
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣x+b的图象与反比例函数![]() (k>0)的图象相交于A,B两点,与x轴相交于点C(4,0),且点B(3,n),连接OB.
(k>0)的图象相交于A,B两点,与x轴相交于点C(4,0),且点B(3,n),连接OB.
(1)求一次函数和反比例函数的表达式;
(2)求△BOC的面积;
(3)将直线AB向下平移,若平移后的直线与反比例函数的图象只有一个交点,试说明直线AB向下平移了几个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
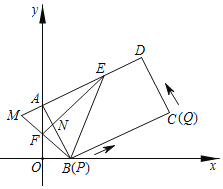
【题目】如图,在直角坐标系中,长方形ABCD(每个内角都是90°)的顶点的坐标分别是A(0,m),B(n,0),(m>n>0),点E在AD上,AE=AB,点F在y轴上,OF=OB,BF的延长线与DA的延长线交于点M,EF与AB交于点N.
(1)试求点E的坐标(用含m,n的式子表示);
(2)求证:AM=AN;
(3)若AB=CD=12cm,BC=20cm,动点P从B出发,以2cm/s的速度沿BC向C运动的同时,动点Q从C出发,以vcm/s的速度沿CD向D运动,是否存在这样的v值,使得△ABP与△PQC全等?若存在,请求出v值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com