
【题目】如图(1),在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,如图(2),设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
(1)求证:BD1=CE1;(2)当∠CPD1=2∠CAD1时,求CE1的长;
(3)连接PA,△PAB面积的最大值为 .(直接填写结果)

【答案】(1)证明见解析(2)![]() (3)2+2
(3)2+2![]()
【解析】试题分析:(1)先求证AC=AB,再由中点可得出结果;
(2)由(1)的结论,在利用勾股定理计算即可;
(3)作出辅助线,利用勾股定理建立方程求出即可.
试题解析:
(1)∵∠A=90°,∠B=45°,
∴∠C=45°,
∴∠C=∠B ,
∴AC=AB,
∵D,E分别是AB,AC的中点 ,
∴CE= ![]() AC, BD=
AC, BD=![]() AB
AB
∴BD= CE
(2)由(1)知△ABD1≌△ACE1,可证∠CPD1=90°,
∴∠CAD1=45°,∠BAD1=135°
在△ABD1中,可以求得BD12=20+8![]()
∴CE12=20+8![]()
(3) 作PG⊥AB,交AB所在直线于点G,如图
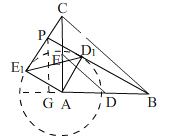
∵D1,E1在以A为圆心,AD为半径的圆上,
当BD1所在直线与⊙A相切时,直线BD1与CE1的交点P到直线AB的距离最大,
此时四边形AD1PE1是正方形,PD1=2,
则BD1=![]()
∴∠ABP=30°,
∴PB=2+![]()
∴点P到AB所在直线的距离的最大值为:PG=1+![]() ,
,
∴△PAB的面积最大值为![]() AB×PG=2+
AB×PG=2+![]() .
.
故答案是:2+![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.全等三角形的三条边相等,三个角也相等
B.判定两个三角形全等的条件中至少有一个是等边
C.面积相等的两个图形是全等形
D.全等三角形的面积和周长都相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知P1(﹣1,y1),P2(2,y2)是一次函数y=﹣x+1图象上的两个点,则y1 , y2的大小关系是( )
A.y1=y2
B.y1<y2
C.y1>y2
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,三个顶点的坐标分别为A(2,2),B(1,0),C(3,1).=

①将△ABC关于x轴作轴对称变换得△A1B1C1,则点C1的坐标为 ;
②将△ABC绕原点O按逆时针方向旋转90°得△A2B2C2,则点C2的坐标为 ;
③△A1B1C1与△A2B2C2成中心对称吗?若成中心对称,则对称中心的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两班共有98人,若从甲班调3人到乙班,那么两班人数正好相等.设甲班原有人数是x人,可列出方程( )
A.98+x=x﹣3
B.98﹣x=x﹣3
C.(98﹣x)+3=x
D.(98﹣x)+3=x﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:满足(1)各边互不相等且均为整数;(2)最短边上的高与最长边上的高的比值为整数k,这样的三角形称为“比高三角形”,其中k叫做“比高系数”.那么周长为13的三角形的“比高系数”k=____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com