
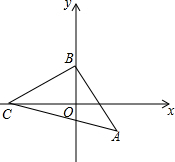
 如图,已知B(0,1),C(-2,0),过点B作AB⊥BC,使得AB=BC.
如图,已知B(0,1),C(-2,0),过点B作AB⊥BC,使得AB=BC.分析 (1)过A点作AE⊥y轴垂足为点E,根据全等三角形的判定证出△BOC≌△EA,再根据全等三角形的性质得出BE=OC,AE=OB,解答即可;
(2)先根据勾股定理求出BC,即可求出△BCP的面积S;
(3)把S=$\frac{10}{3}$代入(2)中的解析式即可求得t的值,证明△OCB≌△OCD,即可求出D的坐标,然后根据待定系数法求得直线AB,CD的解析式,解解析式组成的方程组即可得出P坐标.
解答 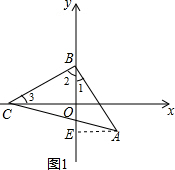 解:(1)过A点作AE⊥y轴,垂足为点E,如图1所示:
解:(1)过A点作AE⊥y轴,垂足为点E,如图1所示:
则∠AEB=90°,
∵B(0,1),C(-2,0),
∴BO=1,CO=2,
∵AB⊥BC,
∴∠ABC=90°,
∴∠1+∠2=90°,
∵∠BOC=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
在△ABE和△BCO中,
$\left\{\begin{array}{l}{∠AEB=∠BOC}\\{∠1=∠3}\\{AB=BC}\end{array}\right.$,
∴△ABE≌△BCO(AAS),
∴AE=BO=1,BE=CO=2,
∵OB=1,
∴OE=1
∴A(1,-1);
(2)根据题意得:AP=t,
由勾股定理得:BC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴△BCP的面积S=$\frac{1}{2}$BP•BC=$\frac{1}{2}$t•$\sqrt{5}$=$\frac{\sqrt{5}}{2}$t;
(3)如图2所示,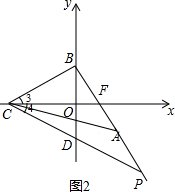
∵S=$\frac{10}{3}$,
∴$\frac{\sqrt{5}}{2}$t=$\frac{10}{3}$,
解得t=$\frac{4\sqrt{5}}{3}$,
∵A(1,-1),B(0,1),
∴直线AB的解析式为y=-2x+1,
∵x轴平分∠BCP,
∴∠3=∠DCO,
在△OCB和△OCD中,
$\left\{\begin{array}{l}{∠3=∠DCO}\\{OC=OC}\\{∠BOC=∠DOC}\end{array}\right.$,
∴△OCB≌△OCD(ASA),
∴OB=OD=1,
∴D(0,-1),
∵C(-2,0),
∴直线CD的解析式为y=-$\frac{1}{2}$x-1,
解$\left\{\begin{array}{l}{y=-2x+1}\\{y=-\frac{1}{2}x-1}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{4}{3}}\\{y=-\frac{5}{3}}\end{array}\right.$,
∴P($\frac{4}{3}$,-$\frac{5}{3}$).
点评 本题考查了全等三角形的判定与性质、勾股定理以及三角形面积的求法、坐标与图形性质;通过作辅助线构造三角形全等是解决问题的关键.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:解答题
 某建筑工程队,在工地一边的靠墙处,用120米长的铁栅栏围成一个所占面积为长方形的临时仓库,已知墙的长度为60米,铁栅栏只围三边,如图所示,设所围成的长方形的面积为1600平方米,求长方形的宽x为多少米?
某建筑工程队,在工地一边的靠墙处,用120米长的铁栅栏围成一个所占面积为长方形的临时仓库,已知墙的长度为60米,铁栅栏只围三边,如图所示,设所围成的长方形的面积为1600平方米,求长方形的宽x为多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
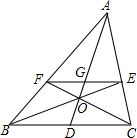 如图,已知△ABC,点E在边AC上,点F在边AB上,EF∥BC,BE与CF交于点O,连接AO交EF于点G,延长AO交BC于点D,求证:BD=CD,EG=FG.
如图,已知△ABC,点E在边AC上,点F在边AB上,EF∥BC,BE与CF交于点O,连接AO交EF于点G,延长AO交BC于点D,求证:BD=CD,EG=FG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
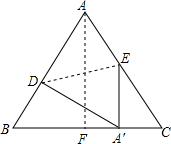 如图,△ABC是正三角形,点E是AC边上的中点,将三角形的一部分沿着DE折叠,使得点A于BC边上的某一点A′重合,若∠BEA′-∠A′EC=∠BAC,求∠ADE.
如图,△ABC是正三角形,点E是AC边上的中点,将三角形的一部分沿着DE折叠,使得点A于BC边上的某一点A′重合,若∠BEA′-∠A′EC=∠BAC,求∠ADE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com