
【题目】在平面直角坐标系中,己知O为坐标原点,点A(3,0),B(0,4),以点A为旋转中心,把△ABO顺时针旋转,得△ACD.记旋转角为α.∠ABO为β.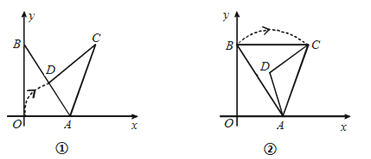
(Ⅰ)如图①,当旋转后点D恰好落在AB边上时,求点D的坐标;
(Ⅱ)如图②,当旋转后满足BC∥x轴时,求α与β之间的数量关系:
(Ⅲ)当旋转后满足∠AOD=β时,求直线CD的解析式(直接写出结果即可).
【答案】解: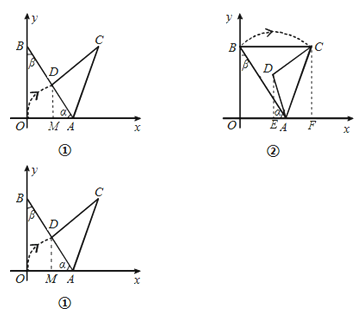
(1)∵点A(3,0),B(0,4),得OA=3,OB=4,
∴在Rt△AOB中,由勾股定理,得AB=![]() =5,
=5,
根据题意,有DA=OA=3.
如图①,过点D作DM⊥x轴于点M,
则MD∥OB,
∴△ADM∽△ABO.有![]()
得![]() ,
,
∴OM=![]() ,
,
∴MD=![]() ,
,
∴点D的坐标为(![]() ,
,![]() ).
).
(2)如图②,由已知,得∠CAB=α,AC=AB,
∴∠ABC=∠ACB,
∴在△ABC中,
∴α=180°﹣2∠ABC,
∵BC∥x轴,得∠OBC=90°,
∴∠ABC=90°﹣∠ABO=90°﹣β,
∴α=2β;
(3)若顺时针旋转,如图,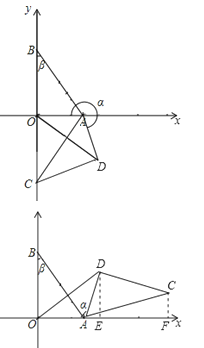
过点D作DE⊥OA于E,过点C作CF⊥OA于F,
∵∠AOD=∠ABO=β,
∴tan∠AOD=![]() =
=![]() ,
,
设DE=3x,OE=4x,
则AE=4x﹣3,
在Rt△ADE中,AD2=AE2+DE2 ,
∴9=9x2+(4x﹣3)2 ,
∴x=![]() ,
,
∴D(![]() ,
,![]() ),
),
∴直线AD的解析式为:y=![]() x﹣
x﹣![]() ,
,
∵直线CD与直线AD垂直,且过点D,
∴设y=﹣![]() x+b,把D(
x+b,把D(![]() ,
,![]() )代入得,
)代入得,![]() =﹣
=﹣![]() ×
×![]() +b,
+b,
解得b=4,
∵互相垂直的两条直线的斜率的积等于﹣1,
∴直线CD的解析式为y=﹣![]() X+4.
X+4.
同理可得直线CD的另一个解析式为y=![]() x﹣4.
x﹣4.
【解析】(1)过点D作DM⊥x轴于点M,求证△ADM∽△ABO,根据相似比求AM的长度,推出OM和MD的长度即可;
(2)根据等腰三角形的性质,推出α=180°﹣2∠ABC,结合已知条件推出∠ABC=90°﹣∠ABO=90°﹣β,即α=2β;
(3)做过点D作DM⊥x轴于点M,根据勾股定理和△OAB∽△OMD,推出D点的横坐标和纵坐标,然后求出C点坐标,就很容易得到CD的解析式了.
【考点精析】认真审题,首先需要了解确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法),还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】已知△ABC是边长为4的等边三角形,BC在x轴上,点D为BC的中点,点A在第一象限内,AB与y轴的正半轴交与点E,已知点B(﹣1,0).
(1)点A的坐标: , 点E的坐标:;
(2)若二次函数y=﹣ ![]() x2+bx+c过点A、E,求此二次函数的解析式;
x2+bx+c过点A、E,求此二次函数的解析式;
(3)P是AC上的一个动点(P与点A、C不重合)连结PB、PD,设l是△PBD的周长,当l取最小值时,求点P的坐标及l的最小值并判断此时点P是否在(2)中所求的抛物线上,请充分说明你的判断理由.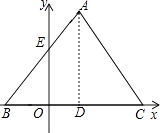
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE= ![]() AC,连接CE,OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( )
AC,连接CE,OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长交AD于E,交BA的延长线于点F.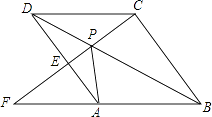
(1)求证:△APD≌△CPD;
(2)求证:△APE∽△FPA;
(3)猜想:线段PC,PE,PF之间存在什么关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区准备新建50个停车位,用以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.6万元;新建3个地上停车位和2个地下停车位共需1.3万元.
(1)该小区新建1个地上停车位和1个地下停车位各需多少万元?
(2)该小区的物业部门预计投资金额超过12万元而不超过13万元,那么共有几种建造停车位的方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】麒麟区第七中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,CD=13m,AD=12m.

(1)求出空地ABCD的面积?
(2)若每种植1平方米草皮需要300元,问总共需投入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R,S,若AQ=PQ,PR=PS,则这四个结论中正确的有( )
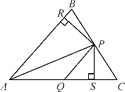
①PA平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP.
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( )

A. BD=DC,AB=AC B. ∠ADB=∠ADC,BD=DC
C. ∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,F为线段DE上一点,且∠AFE=∠B.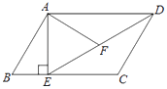
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=3![]() , AF=2
, AF=2![]() , 求AE的长.
, 求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com