
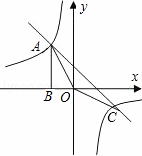
如图,Rt△ABO的顶点A是双曲线y=![]() 与直线y=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=![]() .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.
(1)y=﹣![]() ,y=﹣x+2
,y=﹣x+2
(2)A为(﹣1,3),C为(3,﹣1),面积是4
【解析】
试题分析:(1)欲求这两个函数的解析式,关键求k值.根据反比例函数性质,k绝对值为![]() 且为负数,由此即可求出k;
且为负数,由此即可求出k;
(2)交点A、C的坐标是方程组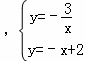 的解,解之即得;
的解,解之即得;
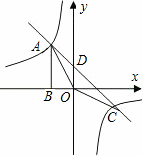
(3)从图形上可看出△AOC的面积为两小三角形面积之和,根据三角形的面积公式即可求出.
解:(1)设A点坐标为(x,y),且x<0,y>0,
则S△ABO=![]() •|BO|•|BA|=
•|BO|•|BA|=![]() •(﹣x)•y=
•(﹣x)•y=![]() ,
,
∴xy=﹣3,
又∵y=![]() ,
,
即xy=k,
∴k=﹣3.
∴所求的两个函数的解析式分别为y=﹣![]() ,y=﹣x+2;
,y=﹣x+2;
(2)由y=﹣x+2,
令x=0,得y=2.
∴直线y=﹣x+2与y轴的交点D的坐标为(0,2),
A、C两点坐标满足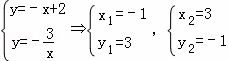
∴交点A为(﹣1,3),C为(3,﹣1),
∴S△AOC=S△ODA+S△ODC=![]() OD•(|x1|+|x2|)=
OD•(|x1|+|x2|)=![]() ×2×(3+1)=4.
×2×(3+1)=4.
点评:此题首先利用待定系数法确定函数解析式,然后利用解方程组来确定图象的交点坐标,及利用坐标求出线段和图形的面积.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
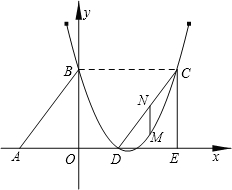 如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=| 2 |
| 3 |
| 5 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |
 象在第四象限的交点,AB⊥x轴于B,且S△ABO=
象在第四象限的交点,AB⊥x轴于B,且S△ABO=| 5 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=
标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=| 2 |
| 3 |
| 5 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,Rt△ABO的顶点A是反比例函数y=
如图,Rt△ABO的顶点A是反比例函数y=| k |
| x |
| 3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com