
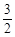 x+b与y轴交于点P,与边OA交于点D,与边BC交于点E.
x+b与y轴交于点P,与边OA交于点D,与边BC交于点E.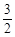 x+b平分矩形OABC的面积,求b的值;
x+b平分矩形OABC的面积,求b的值;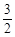 x+b绕点P顺时针旋转时,与直线BC和x轴分别交于点N、M,问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长;若不存在,请说明理由;
x+b绕点P顺时针旋转时,与直线BC和x轴分别交于点N、M,问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长;若不存在,请说明理由;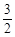 x+b平分矩形OABC的面积,∴其必过矩形的中心
x+b平分矩形OABC的面积,∴其必过矩形的中心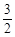 ×6+b
×6+b
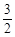 x+12=0解得x=8,∴OD=8
x+12=0解得x=8,∴OD=8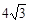 ···················· 6分
···················· 6分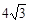 (或由OM=MN解得) 8分
(或由OM=MN解得) 8分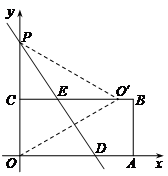
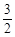 x+a将矩形OABC折叠,点O恰好落在边BC上O′处
x+a将矩形OABC折叠,点O恰好落在边BC上O′处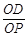
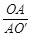
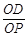 =
=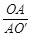 ,即
,即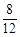 =
=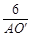 ,AO′=9
,AO′=9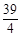 ,12-
,12-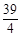 =
=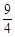
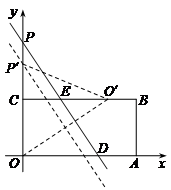
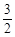 x+12沿y轴向下平移
x+12沿y轴向下平移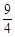 个单位得直线y=-
个单位得直线y=-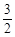 x+
x+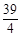 ,将矩形OABC沿直线y=-
,将矩形OABC沿直线y=-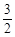 x+
x+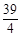 折叠,点O恰好落在边BC上 12分
折叠,点O恰好落在边BC上 12分

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
| 月销量x(件) | 1500 | 2000 |
| 销售价格y(元/件) | 185 | 180 |
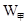 (元)
(元)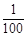 x2元的附加费,设月利
x2元的附加费,设月利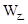 (元)(利润=销售额-成本-附加费).
(元)(利润=销售额-成本-附加费).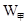 ,
,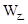 与x间的函数关系式(不必写x的取值范围);
与x间的函数关系式(不必写x的取值范围);查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
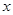 =
=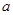 代入,这个函数将失去意义,我们把这样的数值
代入,这个函数将失去意义,我们把这样的数值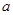 叫做自变量x的奇异值,请写出一个函数,使2和-2都是这个函数的奇异值,你写出的函数为 ▲ .
叫做自变量x的奇异值,请写出一个函数,使2和-2都是这个函数的奇异值,你写出的函数为 ▲ .查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
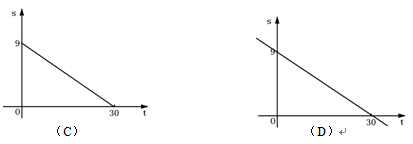
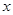 立方米,水费为
立方米,水费为 元,则
元,则 与
与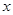 的函数关系用图象表示正确的是( )
的函数关系用图象表示正确的是( )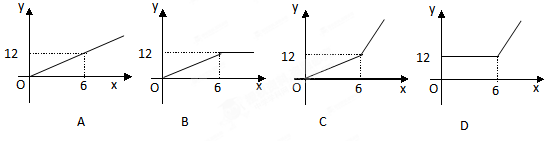
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
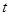 年后该地剩余绿地面积为
年后该地剩余绿地面积为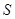 万公顷. 在下列图象中, 能正确反映
万公顷. 在下列图象中, 能正确反映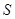 与
与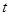 的函数关系的是
的函数关系的是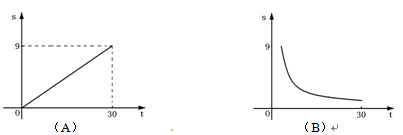
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com