
【题目】![]() ,
,![]() 是平面直角坐标系中的任意两点,我们把
是平面直角坐标系中的任意两点,我们把![]() 叫做P1,P2两点间的“直角距离”,记作d(P1,P2);比如:点P(2,-4),Q(1,0),则d(P,Q)=
叫做P1,P2两点间的“直角距离”,记作d(P1,P2);比如:点P(2,-4),Q(1,0),则d(P,Q)=![]() ,已知Q(2,1),动点P(x,y)满足d(P,Q)=3,且x,y均为整数,则满足条件的点P有________个.
,已知Q(2,1),动点P(x,y)满足d(P,Q)=3,且x,y均为整数,则满足条件的点P有________个.
 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】已知双曲线![]() 与直线
与直线![]() 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线![]() 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线![]() 于点E,交BD于点C.
于点E,交BD于点C.
(1)若点D坐标是(-8,0),求A、B两点坐标及k的值.
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p-q的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为建设国家森林城市,园林部门决定搭配A.B两种园艺造型共50个摆放在市区,现有3490盆甲种花卉和2950盆乙种花卉可供使用,已知搭配一个A种造型需甲种花卉80盆,乙种花卉40盆,搭配一个B种造型需甲种花卉50盆,乙种花卉90盆.
(1)问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个A种造型的费用是800元,搭配一个B种造型的费用是960元,试说明(1)中哪种方案费用最低?最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△OAB的直角边OA在x轴上,顶点B的坐标为(6,8),直线CD交AB于点D(6,3),交x轴于点C(12,0).
(1)求直线CD的函数表达式;
(2)动点P在x轴上从点(﹣10,0)出发,以每秒1个单位的速度向x轴正方向运动,过点P作直线l垂直于x轴,设运动时间为t.
①点P在运动过程中,是否存在某个位置,使得∠PDA=∠B?若存在,请求出点P的坐标;若不存在,请说明理由;
②请探索当t为何值时,在直线l上存在点M,在直线CD上存在点Q,使得以OB为一边,O,B,M,Q为顶点的四边形为菱形,并求出此时t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC∥GE,AF∥DE,∠1=50°.
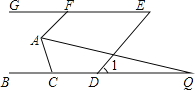
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交BC于点Q,且∠Q=15°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.

(1)如图1,直接写出∠A和∠C之间的数量关系___;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E. F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品,将这些作品排成一个矩形(作品不完全重合),现需要在每张作品的四个角落都钉上图钉,如果作品有角落相邻,那么相邻的角落共享一枚图钉(例如,用9枚图钉将4张作品钉在墙上,如图),若有34枚图钉可供选用,则最多可以展示绘画作品( )
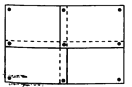
A. 16张 B. 18张 C. 20张 D. 21张
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校学生对以下四个电视节目:![]() 最强大脑
最强大脑![]() 、
、![]() 中国诗词大会
中国诗词大会![]() 、
、![]() 朗读者
朗读者![]() 、
、![]() 出彩中国人
出彩中国人![]() 的喜爱情况,随机抽取了部分学生进行调查,要求每名学生选出并且只能选出一个自己最喜爱的节目,根据调查结果,绘制了如下两幅不完整的统计图.
的喜爱情况,随机抽取了部分学生进行调查,要求每名学生选出并且只能选出一个自己最喜爱的节目,根据调查结果,绘制了如下两幅不完整的统计图.

请你根据图中所提供的信息,完成下列问题:
![]() 本次调查的学生人数为______;
本次调查的学生人数为______;
![]() 在扇形统计图中,A部分所占圆心角的度数为______;
在扇形统计图中,A部分所占圆心角的度数为______;
![]() 请将条形统计图补充完整;
请将条形统计图补充完整;
![]() 若该校共有3000名学生,估计该校最喜爱
若该校共有3000名学生,估计该校最喜爱![]() 中国诗词大会
中国诗词大会![]() 的学生有多少名.
的学生有多少名.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com