
 分别与两坐标轴交于A,B两点,点C从A点出发沿射线BA方向移动,速度为每秒1个单位长度.以C为顶点作等边△CDE,其中点D和点E都在x轴上.半径为
分别与两坐标轴交于A,B两点,点C从A点出发沿射线BA方向移动,速度为每秒1个单位长度.以C为顶点作等边△CDE,其中点D和点E都在x轴上.半径为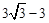 的⊙M与x轴、直线AB相切于点G、F.
的⊙M与x轴、直线AB相切于点G、F.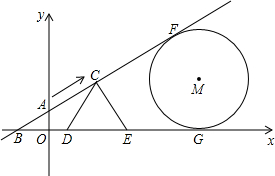
 .
. ,令x=0,则y=1,令y=0,则
,令x=0,则y=1,令y=0,则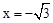 ,∵
,∵ ,∴∠ABO=30°;(2)设点C移动t秒后与⊙M相切,分两种情况讨论,①当CE在⊙M左侧相切于点H;②当CE在⊙M右侧相切于点H,用含t的式子表示出CE,建立方程,解出即可得出答案.
,∴∠ABO=30°;(2)设点C移动t秒后与⊙M相切,分两种情况讨论,①当CE在⊙M左侧相切于点H;②当CE在⊙M右侧相切于点H,用含t的式子表示出CE,建立方程,解出即可得出答案.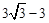 .
.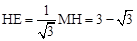 .
. ,∴
,∴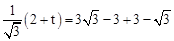 ,解得t=4.
,解得t=4.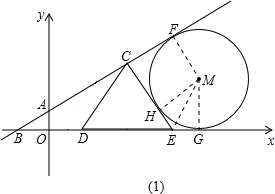
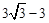 .
.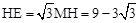 .
. ,解得,t=
,解得,t= .
.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源:不详 题型:解答题

 ;
;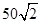 ,∴AB=
,∴AB= .
.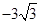 ),C为直线AB上一点,过A、O、C的⊙E的半径为2.求线段OC的长.
),C为直线AB上一点,过A、O、C的⊙E的半径为2.求线段OC的长.
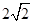 ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连结EF, 设⊙O半径为x, EF为y.①y关于x的函数关系式;②求线段EF长度的最小值.
,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连结EF, 设⊙O半径为x, EF为y.①y关于x的函数关系式;②求线段EF长度的最小值.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
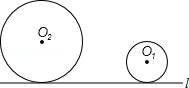
| A.6cm | B.0.5cm | C.3cm | D.2cm |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
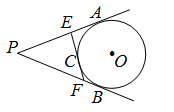
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com