
����Ŀ���Ķ����в��ϣ�
С�Ժ�С��һ����ѧУ���������ˣ���ҵ֮�ʣ�������������乲ͬӵ�е��������Ʋ�����һ�����Ӵʵ䡢һ̨���㳪����һ����ذ�С˵.���DZ��š������ظ��Եļ�ֵƫ�û����Ͻ��е�ֵ���֡���ԭ������˷��䷽�����������£���Ӧ�������������ʾ����
��ÿ�˸��Զ���ÿ����Ʒ�����������Ƶļ�ֵ��
�ڼ���ÿ��������Ʒ������ֵ�;���ֵ�����֣������������ָ��Թ�����ֵ����
��ÿ����Ʒ����۽ϸ������У�
�ܼ������ÿ��������Ʒ�Ĺ�����ֵ�����ֵ֮���
��С����225Ԫ��С�ԣ��ԡ�ʣ�¡���300Ԫÿ�˾���.
���˷��������˷���Ľ���ǣ�С���õ�����ذ�С˵��375ԪǮ��С���õ��ĵ��Ӵʵ�����㳪������Ҫ����375ԪǮ.
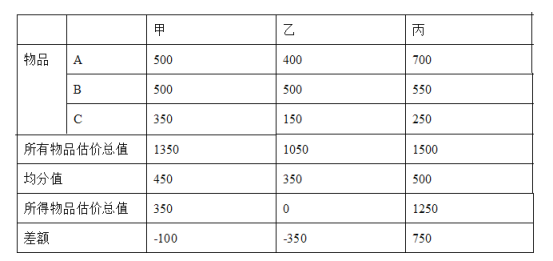
��1���ס��ҡ������˷���A��B��C������Ʒ�����˵Ĺ����������ʾ������������������ֱ��д����������
��2��С���С������D��E������Ʒ�����˵Ĺ����������ʾ������0��m-n��15��.��������������ǰ�IJ����������������ݡ������ظ��Եļ�ֵƫ�û����Ͻ��е�ֵ���֡���ԭ����ô�����Ϊ����������ɱ��ģ���д��������.��˵������������е���ֵ�ĵ�λ��Ϊ��Ԫ����

���𰸡���1���ף��õ���ƷC��200Ԫ���ң��õ�:450Ԫ�������õ���ƷA��B������650Ԫ����2���������.
��������
��1�����շ��䷽���IJ�����з��伴�ɣ�
��2�����շ��䷽���IJ�����з��伴��.
��:��1�����±���
�ʷ���������:
��:�õ���ƷC���ֽ�:![]() Ԫ.
Ԫ.
��:�õ��ֽ�![]() Ԫ.
Ԫ.
��:�õ���ƷA��B,�����ֽ�![]() Ԫ.
Ԫ.
�ʴ�Ϊ��
��:�õ���ƷC���ֽ�: 200Ԫ.
��:�õ��ֽ�450Ԫ.
��:�õ���ƷA��B,����650Ԫ.
��2��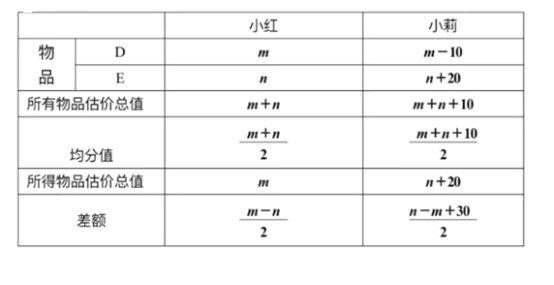
��Ϊ0<m-n<15
����![]()
����![]()
��������Ʒ��С���õġ���ֵ"��С���.�߳�������Ϊ: ![]()
����С�����ã�![]() ��Ԫ��С��.
��Ԫ��С��.
���Է�����Ϊ:С���õ���ƷD�ͣ�![]() ��ԪǮ��С���õ���ƷE��������
��ԪǮ��С���õ���ƷE��������![]() ��ԪǮ.
��ԪǮ.


 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
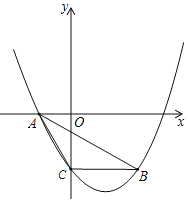
����Ŀ����ͼ��������y��ax2+bx��4����A����3��0����B��5����4�����㣬��y�ύ�ڵ�C������AB��AC��BC��
��1���������ߵı���ʽ��
��2������ABC�������
��3�������ߵĶԳ������Ƿ���ڵ�M��ʹ����ABM��ֱ�������Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�O�У���CΪ![]() ���е㣬��ACB��120����OC���ӳ�����AD���ڵ�D���ҡ�D����B��
���е㣬��ACB��120����OC���ӳ�����AD���ڵ�D���ҡ�D����B��
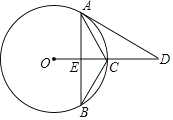
��1����֤��AD���O���У�
��2����CE��4������AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�����κ���ͼ���ϲ��ֵ�ĺ�����x��������y�Ķ�Ӧֵ���±���ʾ��
x | �� | ��3 | ��2 | ��1 | 0 | 1 | �� |
y | �� | 0 | ��3 | ��4 | ��3 | 0 | �� |
��1����������κ����ı���ʽ��
��2���ڸ�����ƽ��ֱ������ϵ�л���������κ�����ͼ��
��3����4��x��1ʱ��ֱ��д��y��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������⡰��ͬԲ�У���ȵ�Բ�Ľ����ԵĻ���ȣ����Ե���Ҳ��ȡ���д�ɡ���֪������֤����������ʽ��������ȷ���ǣ� ��
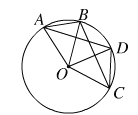
A.��֪���ڡ�O�У���AOB=��COD����AB=��CD.��֤��AB=CD
B.��֪���ڡ�O�У���AOB=��COD����AB=��BC.��֤��AD=BC
C.��֪���ڡ�O�У���AOB=��COD.��֤����AD=��BC��AD=BC
D.��֪���ڡ�O�У���AOB=��COD.��֤����AB=��CD��AB=CD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����У�Ļ��������У����꼶��1������1��������2��Ů�����������������2��������2��Ů��������ֽ�.
��1���ӻ�������������ֽ���7��ѧ����ѡȡ1���μӰ佱��ᣬǡ��ѡ�������� �¼�����������Ȼ����ѡ�������ĸ����� .
��2���ֱ�ӻ�������������ֽ���ѧ���и�ѡȡ1���μӰ佱��ᣬ���б�����״ͼ�ķ�������պ���һ������һŮ���ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��3��AC��4��BC��6��D��BC��һ�㣬CD��2������D��ֱ��l����ABC�ֳ������֣�ʹ�����ֳɵ�����������ABC���ƣ���ֱ��l����ABC��һ�ߵĽ���Ϊ��P����DP��________��
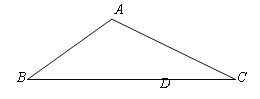
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�������
��������![]() ������
������![]() ��
��![]() .
.
��1����������ߵĺ�������ʽ���Գ��
��2�����![]() ����ԭ��ĶԳƵ�Ϊ
����ԭ��ĶԳƵ�Ϊ![]() ����
����![]() �������߶Գ�����һ���㣬����������
�������߶Գ�����һ���㣬����������![]() ��
��![]() ֮��IJ���Ϊͼ��
֮��IJ���Ϊͼ��![]() ������
������![]() ��
��![]() ���㣩�����ֱ��
���㣩�����ֱ��![]() ��ͼ��
��ͼ��![]() ��һ�������㣬��Ϻ�����ͼ��ֱ��д����
��һ�������㣬��Ϻ�����ͼ��ֱ��д����![]() ������
������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�һ̨�Ʒ�����ˮƽ�����ϣ�����AB�����洹ֱ��������AB��5cm������BC��CD��20cm��BC��CD��ABʼ����ͬһƽ���ڣ�
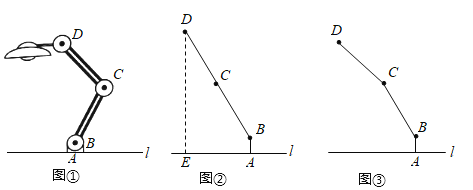
��1����ͼ�ڣ�ת������BC��CD��ʹ��BCD��ƽ�ǣ���ABC��143���������˶˵�D������l�ĸ߶�DE��
��2����ͼ���е�����CD���Ƶ�C��ʱ����ת16������ͼ�ۣ���ʱ���˶˵�D������l�ĸ߶ȼ�С���� ��cm��
���ο����ݣ�sin37����0.6��cos37����0.8��tan37����0.75��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com