
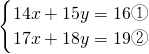 ĘąĢŽÓÉÓÚxĄĒyĩÄÏĩĘýž°ģĢĘýÏîĩÄĘýÖĩ―ÏīóĢŽČįđûÓÃģĢđæĩÄīúČëÏûÔŠ·ĻĄĒžÓžõÏûÔŠ·ĻĀī―âĢŽÄĮ―ŦĘĮžÆËãÁŋīóĢŽĮŌŌŨģöÏÖÔËËãīíÎóĢŽķøēÉÓÃÏÂÃæĩÄ―â·ĻÔōąČ―ÏžōĩĨĢš
ĘąĢŽÓÉÓÚxĄĒyĩÄÏĩĘýž°ģĢĘýÏîĩÄĘýÖĩ―ÏīóĢŽČįđûÓÃģĢđæĩÄīúČëÏûÔŠ·ĻĄĒžÓžõÏûÔŠ·ĻĀī―âĢŽÄĮ―ŦĘĮžÆËãÁŋīóĢŽĮŌŌŨģöÏÖÔËËãīíÎóĢŽķøēÉÓÃÏÂÃæĩÄ―â·ĻÔōąČ―ÏžōĩĨĢš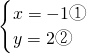
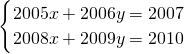
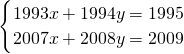 ĩÄ―âĘĮ________Ģŧ
ĩÄ―âĘĮ________Ģŧ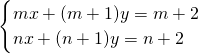 ĢĻmĄŲnĢĐĩÄ―âĘĮĘēÃīĢŋēĒÓ÷―ģĖŨéĩÄ―âžÓŌÔŅéÖĪĢŪ
ĢĻmĄŲnĢĐĩÄ―âĘĮĘēÃīĢŋēĒÓ÷―ģĖŨéĩÄ―âžÓŌÔŅéÖĪĢŪ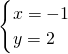
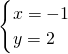
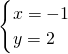
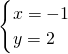 ĘĮÔ·―ģĖŨéĩÄ―âĢŪ
ĘĮÔ·―ģĖŨéĩÄ―âĢŪ


| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢšÔÄķÁĀí―â
|
|
|
|
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢšÔÄķÁĀí―â
|
|
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢšÔÄķÁĀí―â
|
|
|
|
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢšÔÄķÁĀí―â
|
|
|
|
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢšÔÄķÁĀí―â
|
|
|
|
ēéŋīīð°ļšÍ―âÎö>>
°ŲķČÖÂÐÅ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com