
【题目】点A,B在数轴上表示的数如图所示. 动点P从点A出发,沿数轴向右以每秒2个单位长度的速度运动到点B,再从点B以同样的速度运动到点A停止,设点P运动的时间为t秒,解答下列问题.
![]()
(1)当t=2时,AP= 个单位长度,当t=6时,AP= 个单位长度;
(2)直接写出整个运动过程中AP的长度(用含t的代数式表示);
(3)当AP=6个单位长度时,求t的值;
(4)当点P运动到线段AB的3等分点时,t的值为 .
【答案】(1)4, 8;(2)2t个单位长度或20-2t个单位长度;(3)t=3或7;(4)![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)当t=2时,列式计算即可;当t=6时,点P到达点B,而且从点B向左运动1秒,即可求出答案;
(2)根据题意,可分为两个过程,点P从点A运动到点B,和从点B运动回点A,进行分类讨论,即可得到答案;
(3)当AP=6,分别代入(2)中的结论,即可求出答案;
(4)根据题意,AB的三等分点有两个点,可分为4种情况进行分析,即可得到答案.
解:(1)根据题意,![]() ,
,
∴点P从点A运动到点B需要:![]() 秒;
秒;
∴当t=2时,![]() ;
;
当t=6时,![]() ;
;
故答案为:4,8 .
(2)根据题意,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
∴整个运动过程中AP的长度为:2t个单位长度或![]() 个单位长度;
个单位长度;
(3)∵AP=6,
当2t=6时,解得:t=3;
当20-2t=6时,解得:t=7;
(4)∵AB=10,
①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() ;
;
③当![]() 时,
时,![]() ;
;
④当![]() 时,
时,![]() ;
;
综上所述,t的值为:或
![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
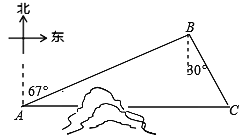
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地,现计划开凿隧道使A、C两地直线贯通,经测量得:B地在A地的北偏东67°方向,距离A地280km,C地在B地南偏东的30°方向.
(1)求B地到直线AC的距离;
(2)求隧道开通后与隧道开通前相比,从A地到C地的路程将缩短多少?
(本题结果都精确到0.1km)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】梯形ABCD中AB∥CD,∠ADC+∠BCD=90°,以AD、AB、BC为斜边向形外作等腰直角三角形,其面积分别是![]() ,且
,且![]() ,则CD=( )
,则CD=( )

A.2.5ABB.3ABC.3.5ABD.4AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,点E为AD上一点,BE ⊥ AC于F点.

(1)若AE=![]() AD,△AEF的面积为1时,求△ABC的面积;
AD,△AEF的面积为1时,求△ABC的面积;
(2)若AD = 4,tan∠EAF =![]() ,求AF的长;
,求AF的长;
(3)若tan∠EAF =![]() ,连接DF,证明DF=AB.
,连接DF,证明DF=AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内,将一副直角三角板按如图所示的方式摆放,其中三角形ABC为含60°角的直角三角板,三角形BDE为含45°角的直角三角板.

(1)如图1,若点D在AB上,则∠EBC的度数为 ;
(2)如图2,若∠EBC=170°,则∠α的度数为 ;
(3)如图3,若∠EBC=118°,求∠α的度数;
(4)如图3,若0°<∠α<60°,求∠ABE-∠DBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一些数学问题的研究可以经历观察、探究、发现、证明等过程.下面是对一个问题的部分研究过程:
(观察)![]() =
=![]() ,
,![]() =
=![]() ,
,![]() 是否也能写成分数的形式?
是否也能写成分数的形式?
(探究1)设![]() =x,
=x,
由![]() =0.555…可知,10x=5.555…,
=0.555…可知,10x=5.555…,
所以10x﹣x=5.
解方程,得x=![]()
于是,得![]() =
=![]() .
.
所以,![]() 能写成分数的形式
能写成分数的形式
(探究2)仿照上面的方法,尝试将![]() 写成分数的形式.
写成分数的形式.
(发现) .
请你完成(探究2)的部分,并用一句话概括你的发现
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在直线AB上,OC⊥AB .在RtΔODE中,∠ODE=90°,∠DOE=30°,先将ΔODE一边OE与OC重合(如图1),然后将ΔODE绕点O按顺时针方向旋转(如图2),当OE与OC 重合时停止旋转.
(1)当∠AOD=80°时,则旋转角∠COE的大小为____________ ;
(2)当OD在OC与OB之间时,求∠AOD![]() ∠COE的值;
∠COE的值;
(3)在ΔODE的旋转过程中,若∠AOE=4∠COD时,求旋转角∠COE的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求1+2+22+23+24+25+26的值时,小明发现:从第二个加数起每一个加数都是前一个加数的2倍,于是他设:S=1+2+22+23+24+25+26①然后在①式的两边都乘以2,得:2S=2+22+23+24+25+26+27 ②;②﹣①得2S﹣S=27﹣1,S=27﹣1,即1+2+22+23+24+25+26=27﹣1.
(1)求1+3+32+33+34+35+36的值;
(2)求1+a+a2+a3+…+a2013(a≠0且a≠1)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com