
分析 分两种情况讨论:①点P的路径是一段弧,由题目不难看出当D为AC的中点的时候,点P经过弧AB的中点,此时△ABP为等腰三角形,继而求得半径和对应的圆心角的度数,求得答案.②点E靠近点B时,点P的路径就是过点C向AB做的垂线段.
解答 解:若AE=BD,则有AD=BE或AD=CE两种情况:
①当AD=CE时,点P的路径是一段弧,当D为AC的中点的时候,点P经过弧AB的中点,
此时△ABP为等腰三角形,且∠ABP=∠BAP=30°,
∴∠AOB=120°,
又∵AB=18,
∴OA=6$\sqrt{3}$,
∴点P的路径长l=$\frac{120×π×6\sqrt{3}}{180}$=4$\sqrt{3}$π;
②当AD=BE时,点P的路径就是过点C向AB作的垂线段CG,
因为等边三角形ABC的边长为18,
所以点P的路径长CG为:9$\sqrt{3}$.
故答案为:4$\sqrt{3}$π或9$\sqrt{3}$.
点评 本题考查了等边三角形的性质的运用,全等三角形的判定及性质的运用,弧线长公式的运用,解答时证明三角形全等是关键,解答本题时注意转化思想的运用.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
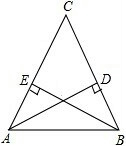 如图,从C地看A,B两地的视角∠C是锐角,从C地到A,B两地的距离相等,A地到路段BC的距离AD与B地到路段AC的距离BE相等吗?为什么?
如图,从C地看A,B两地的视角∠C是锐角,从C地到A,B两地的距离相等,A地到路段BC的距离AD与B地到路段AC的距离BE相等吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
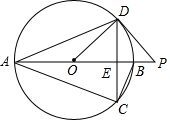 已知:如图,AB是⊙O的直径,CD是弦,且AB⊥CD于E,P是AB延长线上一点,连接PD,∠PDC=∠CAD.
已知:如图,AB是⊙O的直径,CD是弦,且AB⊥CD于E,P是AB延长线上一点,连接PD,∠PDC=∠CAD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知一次函数y=mx的图象经过点A(-2,4),点A关于y轴的对称点B在反比例函数y=$\frac{k}{x}$的图象上.
如图,已知一次函数y=mx的图象经过点A(-2,4),点A关于y轴的对称点B在反比例函数y=$\frac{k}{x}$的图象上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{AB}{DE}$=$\frac{AC}{DF}$ | B. | $\frac{AB}{DE}$=$\frac{BC}{EF}$ | C. | ∠A=∠E | D. | ∠B=∠D |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
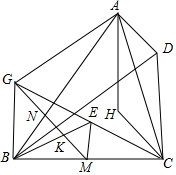 如图,已知H为锐角△ABC的垂心,D是使四边形AHCD为平行四边形的一点,过BC的中点M作AB的垂线,垂足为N,K为MN的中点,过点A作BD的平行线交MN于点G,若A,K,M,C四点共圆.求证:直线BK平分线段CG.
如图,已知H为锐角△ABC的垂心,D是使四边形AHCD为平行四边形的一点,过BC的中点M作AB的垂线,垂足为N,K为MN的中点,过点A作BD的平行线交MN于点G,若A,K,M,C四点共圆.求证:直线BK平分线段CG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com