
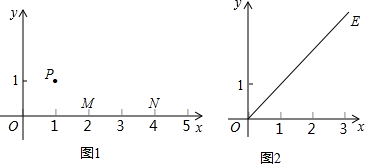
 ,且点G的横坐标为1,试求点G的纵坐标.
,且点G的横坐标为1,试求点G的纵坐标.
 ,
, ;
; ,
, ,由勾股定理得G1K=2,
,由勾股定理得G1K=2, ,
, .
. ,求出GK的长,根据GK+KH求出GH的长,即为G1的纵坐标;②如图2所示,过点O作G2O⊥OE交直线x=1于点G2,由题意知△OHG2为等腰直角三角形,由OH的长求出HG2的长,即为G2的纵坐标,综上,得到所有满足题意G的纵坐标.
,求出GK的长,根据GK+KH求出GH的长,即为G1的纵坐标;②如图2所示,过点O作G2O⊥OE交直线x=1于点G2,由题意知△OHG2为等腰直角三角形,由OH的长求出HG2的长,即为G2的纵坐标,综上,得到所有满足题意G的纵坐标.

科目:初中数学 来源: 题型:
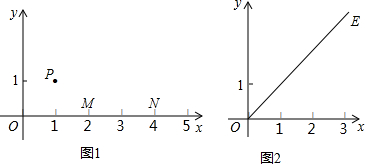
 23、在方格纸上画图并回答问题.如图,已知线段AB及点C.
23、在方格纸上画图并回答问题.如图,已知线段AB及点C.查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:活学巧练七年级数学(上) 题型:013
下列说法中,正确的是
[ ]
A.已知线段AB及点P,过P和线段AB的中点作AB的垂线
B.已知线段AB及点P,过P作AB的垂线
C.已知直线AB∥CD及点P,过P作直线MN,使MN∥AB,MN∥CD
D.已知直线AB及点P,过P作直线MN,使MN⊥AB
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
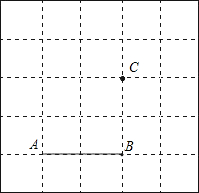 在方格纸上画图并回答问题.如图,已知线段AB及点C.
在方格纸上画图并回答问题.如图,已知线段AB及点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com