
| A. | 一定相似 | B. | 一定不相似 | C. | 不一定相似 | D. | 以上说法都不对 |
分析 先假设两矩形和原矩形相似,得出比例式,求出原矩形的长和宽的比,即可得出选项.
解答 解:∵假如矩形AEFB∽矩形ABCD,
∴$\frac{AE}{AB}$=$\frac{AB}{AD}$,
设AD=x,AB=y,则AE=$\frac{1}{2}$x.则 $\frac{\frac{1}{2}x}{y}$=$\frac{y}{x}$,
∴$\frac{{x}^{2}}{{y}^{2}}$=2.
∴x:y=$\sqrt{2}$:1.
即原矩形长与宽的比为 $\sqrt{2}$:1,
即当原矩形长与宽的比为 $\sqrt{2}$:1时,这两个矩形与原矩形相似,否则就不相似,
故选C.
点评 本题考查了相似多边形的性质的应用,能根据相似多边形的性质得出比例式是解此题的关键,根据相似形的对应边的比相等,把几何问题转化为方程问题,正确分清对应边,以及正确解方程是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | sin35°+sin45°=sin80° | B. | cos30°+cos15°=cos45° | ||
| C. | tan60°+cos22°=tan82° | D. | tan30°=$\frac{sin30°}{cos30°}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
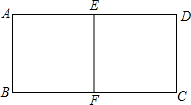 如图,把一个矩形纸片ABCD沿AD和BC的中点连线EF对折,要使矩形AEFB与原矩形相似,则原矩形长与宽的比为( )
如图,把一个矩形纸片ABCD沿AD和BC的中点连线EF对折,要使矩形AEFB与原矩形相似,则原矩形长与宽的比为( )| A. | 2:1 | B. | 3:1 | C. | $\sqrt{2}$:1 | D. | 4:1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一油桶高1m,桶内有油,一根木棒长1.2m,从桶盖的小口处斜插入桶内,一端插到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长为0.48m,求桶内油面的高度.
如图,一油桶高1m,桶内有油,一根木棒长1.2m,从桶盖的小口处斜插入桶内,一端插到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长为0.48m,求桶内油面的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com