
【题目】如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度i=1: ![]() ,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°.
,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°. 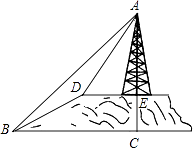
(1)求小山的高度;
(2)求铁架的高度.( ![]() ≈1.73,精确到0.1米)
≈1.73,精确到0.1米)
【答案】
(1)解:如图,过D作DF垂直于坡底的水平线BC于点F.
由已知,斜坡的坡比i=1: ![]() ,于是tan∠DBC=
,于是tan∠DBC= ![]() ,
,
∴坡角∠DBC=30°.
于是在Rt△DFB中,DF=DBsin30°=25,
即小山高为25米

(2)解:设铁架的高AE=x.
在Rt△AED中,已知∠ADE=60°,于是DE= ![]() ,
,
在Rt△ACB中,已知∠ABC=45°,
∵AC=AE+EC=AE+DF=x+25,
又BC=BF+FC=BF+DE=25 ![]() x,
x,
由AC=BC,得x+25=25 ![]() x.
x.
∴x=25 ![]() ≈43.3,即铁架高43.3米
≈43.3,即铁架高43.3米
【解析】(1)过D作DF垂直于坡底的水平线BC于点F,再由斜坡的坡比的概念,可得坡角为30°;解Rt△DFB可得DF即山高;(2)首先根据题意分析图形;本题涉及到两个直角三角形Rt△AED与Rt△ACB,解可得AC与BC的大小,再由AC=AE+EC,进而可求出答案.
【考点精析】根据题目的已知条件,利用关于坡度坡角问题和关于仰角俯角问题的相关知识可以得到问题的答案,需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA;仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:
【题目】![]() 在平面直角坐标系中,将点
在平面直角坐标系中,将点![]() 向右平移
向右平移![]() 个单位到点
个单位到点![]() ,再将点
,再将点![]() 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转![]() 到点
到点![]() .直接写出点
.直接写出点![]() ,
,![]() 的坐标;23.
的坐标;23.
![]() 在平面直角坐标系中,将第二象限内的点
在平面直角坐标系中,将第二象限内的点![]() 向右平移
向右平移![]() 个单位到第一象限点
个单位到第一象限点![]() ,再将点
,再将点![]() 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转![]() 到点
到点![]() ,直接写出点
,直接写出点![]() ,
,![]() 的坐标;
的坐标;
![]() 在平面直角坐标系中.将点
在平面直角坐标系中.将点![]() 沿水平方向平移
沿水平方向平移![]() 个单位到点
个单位到点![]() ,再将点
,再将点![]() 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转![]() 到点
到点![]() ,直接写出点
,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为边在AD的右侧作正方形ADEF,连接CF.
(1)观察猜想:如图(1),当点D在线段BC上时,
①BC与CF的位置关系是: ;
②BC、CD、CF之间的数量关系为: (将结论直接写在横线上)
(2)数学思考:如图(2),当点D在线段CB的延长线上时,上述①、②中的结论是否仍然成立?若成立,请给予证明,若不成立,请你写出正确结论再给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,直线MN经过点A,过点B作BD⊥MN于D,过C作CE⊥MN于E.
(1)求证:△ABD≌△CAE;
(2)若BD=12cm,DE=20cm,求CE的长度.
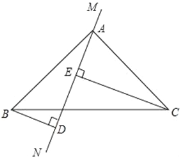
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAD=∠DAC,DF上AB,DM⊥AC,AF=10cm,AC=14cm,动点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.当t=________秒时,△DFE与△DMG全等.
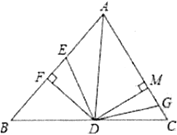
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,△ABC的高CD与角平分线AE相交点F,过点C作CH⊥AE于G,交AB于H.
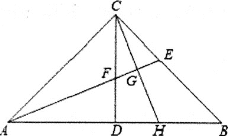
(1)直接写出∠CFE的度数________;
(2)求证:CF=BH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为( )
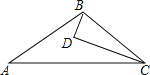
A. 1 B. 1.5 C. 2.5 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com